Liouville equation

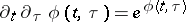
The Liouville equation

(a1)

is a non-linear partial differential equation (cf. Differential equation, partial) that can be linearized and subsequently solved. Namely, it can be transformed into the linear wave equation

(a2)

by any of the following two differential substitutions (see [a1], formulas (4) and (2)):

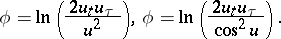(a3)

In other words, the formulas (a3) provide the general solution to the Liouville equation, in terms of the well-known general solution 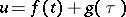of the wave equation (a2).

The Liouville equation appears also in Lie's classification [a2] of second-order differential equations of the form

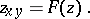(a4)

For the complete classification, see [a4].

The Liouville equation (a1) is invariant under the infinite group of point transformations

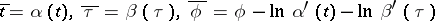(a5)

with arbitrary invertible differentiable functions 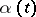and . The infinitesimal generator of this group is:

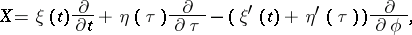where 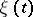, 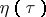are arbitrary functions and 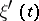, 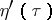are their first derivatives. It is shown in [a2] that the equation (a4), and in particular the Liouville equation, does not admit non-trivial (i.e. non-point) Lie tangent transformations.

In addition to the transformations (a3), it is known (see, e.g., [a3]) that the Liouville equation is related with the wave equation (a2) by the following Bäcklund transformation:

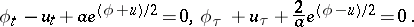By letting 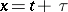, 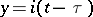in (a1), (a2) and (a3), where , one can transform the elliptic Liouville equation 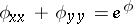into the Laplace equation .

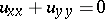References

[a1]	J. Liouville, "Sur l'équation aux différences partielles 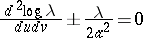" J. Math. Pures Appl. , 8 (1853) pp. 71–72
[a2]	S. Lie, "Discussion der Differentialgleichung 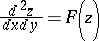" Arch. for Math. , 6 (1881) pp. 112–124 (Reprinted as: S. Lie: Gesammelte Abhandlungen, Vol. 3, pp. 469–478)
[a3]	N.H. Ibragimov, "Transformation groups applied to mathematical physics" , Reidel (1985) (In Russian)
[a4]	"CRC Handbook of Lie group analysis of differential equations" N.H. Ibragimov (ed.) , 1 , CRC (1994) pp. Chapt. 12.3