Diagonal continued fraction

A continued fraction

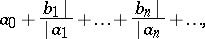in which the sequences 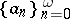and 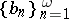must satisfy the following conditions:

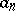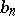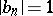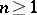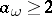1) the numbers and are integers; ; if ; if ;

2) 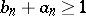for all ; if 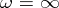, then 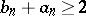for an infinite set of indices ;

3) 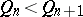for all ;

4) the partial fractions of the continued fraction are all irreducible fractions 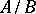such that 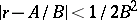and 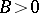, where is value of the continued fraction.

For each real number there exists one and only one diagonal continued fraction with as its value; this fraction is periodic if is a quadratic irrationality.

Comments

After truncation and evaluation one obtains

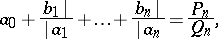with 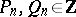, , 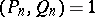. These are the numbers 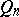alluded to in condition . The continued fraction as described above for a real number 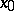can be obtained by the nearest integer algorithm, that is, 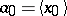, , 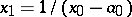, , 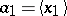, 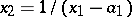etc., where 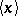denotes the nearest integer to . It is also possible to use the entier function 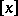instead of 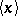. One then has the continued fraction algorithm which is more commonly used.

The adjective "diagonal" stems from the fact that 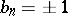for all .

References

[a1]	G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8
[a2]	O. Perron, "Die Lehre von den Kettenbrüchen" , I , Teubner (1977)