Kleene-Mostowski classification
A classification of number-theoretic predicates, introduced independently by S.C. Kleene [1] and A. Mostowski [2]. The class of all recursive predicates is denoted simultaneously by 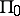 and
and 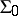 . For each
. For each 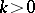 the class
the class 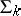 is defined as the class of all predicates expressible in the form
is defined as the class of all predicates expressible in the form 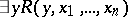 , where
, where 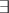 is the existential quantifier and
is the existential quantifier and 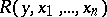 is a predicate in the class
is a predicate in the class 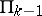 , while the class
, while the class 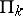 is defined as the class of predicates expressible in the form
is defined as the class of predicates expressible in the form 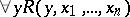 , where
, where 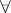 is the universal quantifier and the predicate
is the universal quantifier and the predicate 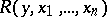 belongs to the class
belongs to the class 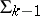 . In this way a double sequence of classes is obtained:
. In this way a double sequence of classes is obtained:
 |
If a predicate belongs to 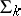 or
or 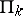 , then it belongs to the classes
, then it belongs to the classes 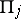 and
and 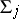 for any
for any 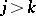 , that is,
, that is, 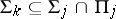 and
and 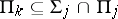 for any
for any 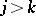 . If
. If 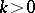 , then there exist predicates in
, then there exist predicates in 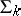 not belonging to
not belonging to 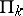 and also predicates in
and also predicates in 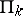 not belonging to
not belonging to 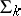 , that is,
, that is, 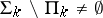 and
and 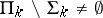 . A predicate belongs to one of the classes
. A predicate belongs to one of the classes 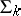 or
or 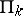 if and only if it is expressible in the language of formal arithmetic (cf. Arithmetic, formal). If a predicate
if and only if it is expressible in the language of formal arithmetic (cf. Arithmetic, formal). If a predicate 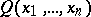 belongs to
belongs to 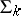 (or
(or 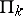 ) then
) then 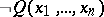 , where
, where  is the negation sign, belongs to
is the negation sign, belongs to 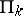 (respectively,
(respectively, 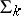 ). A predicate
). A predicate 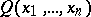 is recursive (cf. Recursive predicate) if and only if
is recursive (cf. Recursive predicate) if and only if 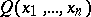 and
and 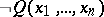 belong to
belong to 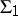 , i.e.
, i.e. 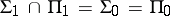 . If
. If 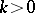 , then
, then 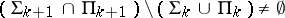 .
.
The classification of sets defined in the language of formal arithmetic is based on the classification of predicates: A set 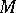 belongs to
belongs to 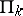 (or
(or 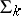 ) if the predicate "x M" belongs to this class.
) if the predicate "x M" belongs to this class.
References
| [1] | S.C. Kleene, "Recursive predicates and quantifiers" Trans. Amer. Math. Soc. , 53 (1943) pp. 41–73 |
| [2] | A. Mostowski, "On definable sets of positive integers" Fund. Math. , 34 (1947) pp. 81–112 |
Comments
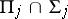 is commonly denoted by
is commonly denoted by 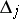 . One usually speaks of the arithmetical hierarchy (rather than the Kleene–Mostowski classification).
. One usually speaks of the arithmetical hierarchy (rather than the Kleene–Mostowski classification).
References
| [a1] | H.B. Enderton, "Elements of recursion theory" J. Barwise (ed.) , Handbook of mathematical logic , North-Holland (1977) pp. 527–566 |
Kleene-Mostowski classification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kleene-Mostowski_classification&oldid=18718