Albanese variety
An Abelian variety 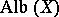 canonically attached to an algebraic variety
canonically attached to an algebraic variety 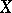 , which is the solution of the following universal problem: There exists a morphism
, which is the solution of the following universal problem: There exists a morphism 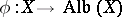 such that any morphism
such that any morphism 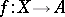 into an Abelian variety
into an Abelian variety  factors into a product
factors into a product 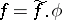 , where
, where 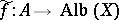 (so named in honour of G. Albanese). If
(so named in honour of G. Albanese). If 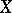 is a complete non-singular variety over the field of complex numbers, the Albanese variety can be described as follows. Let
is a complete non-singular variety over the field of complex numbers, the Albanese variety can be described as follows. Let 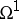 be the space of everywhere-regular differential forms of degree 1 on
be the space of everywhere-regular differential forms of degree 1 on  . Each one-dimensional cycle
. Each one-dimensional cycle 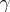 of the topological space
of the topological space 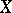 determines a linear function
determines a linear function 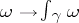 on
on  . The image of the mapping
. The image of the mapping 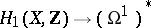 thus obtained is a lattice
thus obtained is a lattice 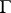 in
in 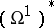 , and the quotient space
, and the quotient space 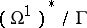 coincides with the Albanese variety of
coincides with the Albanese variety of 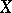 . From the algebraic point of view, an Albanese variety may be considered as a method of defining an algebraic structure on some quotient group of the group
. From the algebraic point of view, an Albanese variety may be considered as a method of defining an algebraic structure on some quotient group of the group 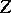 of zero-dimensional cycles of degree 0 on
of zero-dimensional cycles of degree 0 on 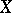 . If
. If 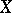 is a non-singular complete algebraic curve, both its Picard variety and its Albanese variety are called its Jacobi variety. If the ground field has characteristic zero, then the equalities
is a non-singular complete algebraic curve, both its Picard variety and its Albanese variety are called its Jacobi variety. If the ground field has characteristic zero, then the equalities
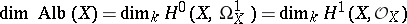 |
are valid. The number 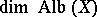 is called the irregularity of the variety
is called the irregularity of the variety 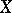 . If the field has finite characteristic, the inequalities
. If the field has finite characteristic, the inequalities
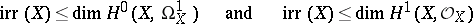 |
hold. If the ground field has positive characteristics it can happen that
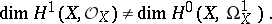 |
The Albanese variety is dual to the Picard variety.
References
| [1] | M. Baldassarri, "Algebraic varieties" , Springer (1956) |
| [2] | S. Lang, "Abelian varieties" , Springer (1983) |
Albanese variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Albanese_variety&oldid=18712