Complexification of a vector space
From Encyclopedia of Mathematics
The complex vector space 
obtained from the real vector space 
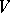by extending the field of scalars. The space 
is defined as the tensor product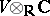 
. It can also be defined as the set of formal expressions 
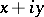, where 
, with the operations of addition and multiplication by complex numbers defined in the usual way. The space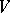 
is contained in 
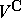as a real subspace and is called a real form of 
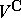. Every basis of 
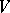is a basis of 
(over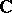 
). In particular, 
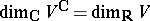. The operation 
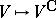is a functor from the category of vector spaces over 
into the category of vector space over 
.
How to Cite This Entry:
Complexification of a vector space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complexification_of_a_vector_space&oldid=18691
Complexification of a vector space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complexification_of_a_vector_space&oldid=18691
This article was adapted from an original article by A.L. Onishchik (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article