Integral transform
A transform of functions, having the form
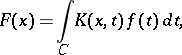 | (1) |
where 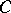 is a finite or infinite contour in the complex plane and
is a finite or infinite contour in the complex plane and 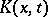 is the kernel of the integral transform (cf. Kernel of an integral operator). In most cases one considers integral transforms for which
is the kernel of the integral transform (cf. Kernel of an integral operator). In most cases one considers integral transforms for which 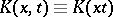 and
and 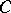 is the real axis or a part
is the real axis or a part  of it. If
of it. If 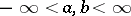 , then the transform is said to be finite. Formulas enabling one to recover the function
, then the transform is said to be finite. Formulas enabling one to recover the function 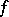 from a known
from a known 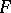 are called inversion formulas of the integral transform.
are called inversion formulas of the integral transform.
Examples of integral transforms. The Bochner transform:
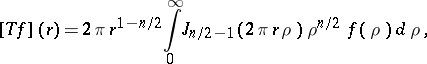 |
where 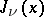 is the Bessel function of the first kind of order
is the Bessel function of the first kind of order  (cf. Bessel functions) and
(cf. Bessel functions) and 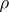 is the distance in
is the distance in  . The inversion formula is:
. The inversion formula is: 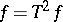 . The Parseval identity is:
. The Parseval identity is:
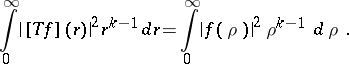 |
The Weber transform:
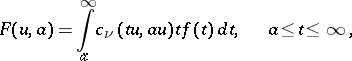 |
where 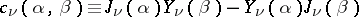 and
and 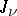 and
and 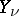 are the Bessel functions of first and second kind. The inversion formula is:
are the Bessel functions of first and second kind. The inversion formula is:
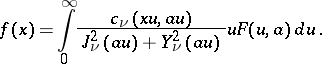 |
For 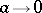 , the Weber transform turns into the Hankel transform:
, the Weber transform turns into the Hankel transform:
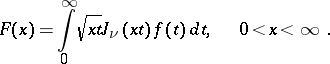 |
For 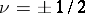 this transform reduces to the Fourier sine and cosine transforms. The inversion formula is as follows: If
this transform reduces to the Fourier sine and cosine transforms. The inversion formula is as follows: If  , if
, if 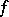 is of bounded variation in a neighbourhood of a point
is of bounded variation in a neighbourhood of a point 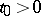 and if
and if 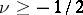 , then
, then
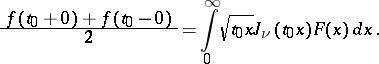 |
The Parseval identity: If 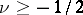 , if
, if 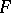 and
and 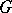 are the Hankel transforms of the functions
are the Hankel transforms of the functions  and
and 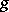 , where
, where 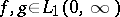 , then
, then
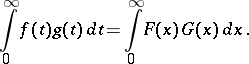 |
Other forms of the Hankel transform are:
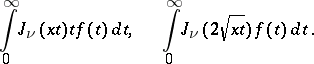 |
The Weierstrass transform:
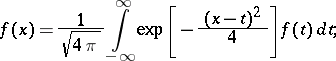 |
it is a special case of a convolution transform.
Repeated transforms. Let
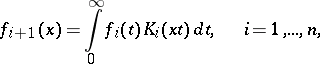 |
where 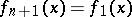 . Such a sequence of integral transforms is called a chain of integral transforms. For
. Such a sequence of integral transforms is called a chain of integral transforms. For  , repeated integral transforms are often called Fourier transforms.
, repeated integral transforms are often called Fourier transforms.
Multiple (multi-dimensional) integral transforms are transforms (1) where 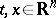 and
and 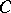 is some domain in the complex Euclidean
is some domain in the complex Euclidean  -dimensional space.
-dimensional space.
Integral transforms of generalized functions can be constructed by the following basic methods:
1) One constructs a space of test functions 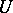 containing the kernel
containing the kernel 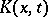 of the integral transform
of the integral transform 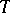 under consideration. Then the transform
under consideration. Then the transform 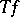 for any generalized function
for any generalized function 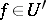 is defined as the value of
is defined as the value of 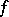 on the test function
on the test function 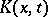 according to the formula
according to the formula
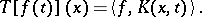 |
2) A space of test functions 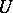 is constructed on which the classical integral transform
is constructed on which the classical integral transform 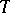 is defined, mapping
is defined, mapping 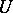 onto some space of test functions
onto some space of test functions 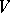 . Then the integral transform
. Then the integral transform 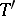 of a generalized function
of a generalized function 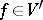 is defined by the equation
is defined by the equation
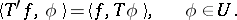 |
3) The required integral transform is expressed in terms of another integral transform that is defined for generalized functions.
See also Convolution transform; Euler transformation; Fourier transform; Gauss transform; Gegenbauer transform; Hardy transform; Hermite transform; Jacobi transform; Kontorovich–Lebedev transform; Mehler–Fock transform; Meijer transform; Mellin transform; Stieltjes transform; Watson transform; Whittaker transform.
References
| [1] | V.A. Ditkin, A.P. Prudnikov, "Operational calculus" Progress in Math. , 1 (1968) pp. 1–75 Itogi Nauk. Mat. Anal. 1966 (1967) pp. 7–82 |
| [2] | Y.A. Brychkov, A.P. Prudnikov, "Integral transforms of generalized functions" , Gordon & Breach (1989) (Translated from Russian) |
| [3] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
Comments
References
| [a1] | I.N. Sneddon, "The use of integral transforms" , McGraw-Hill (1972) |
| [a2] | H. Zemanian, "Generalized integral transformations" , Interscience (1968) |
Integral transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_transform&oldid=18676