Borsuk problem

One of the fundamental problems in combinatorial geometry: Is it possible, for any bounded set of diameter 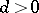in an -dimensional Euclidean space, to make a decomposition into not more than subsets with diameters smaller than 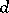? The problem was formulated by K. Borsuk [1] who noted that it was not possible to subdivide an -dimensional simplex and an -dimensional sphere in 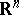into parts of a smaller diameter. The problem has a positive solution for 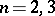, but only partial results have been obtained for . Thus, for instance, the problem has been positively solved for any bounded smooth convex set in 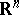[2]. It has been proved that the solution of Borsuk's problem can be reduced to the case of sets of constant width. If 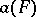is the smallest number of parts of a diameter smaller than 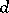into which a set 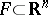can be subdivided, then the equality 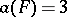is valid for a figure 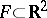of diameter 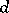if and only if 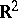contains a unique figure of constant width 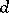containing 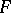[3]. This fact cannot be directly generalized to the case 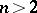. The Borsuk problem is closely related to the illumination problem and to the Hadwiger hypothesis, which is a generalization of the Borsuk problem in which 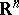is replaced by a finite-dimensional normed space.

References

[1]	K. Borsuk, "Drei Sätze über die -dimensionale euklidische Sphäre" Fund. Math. , 20 (1933) pp. 177–190
[2]	B. Grünbaum, "Borsuk's problem and related questions" V.L. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 271–284
[3]	V.G. Boltyanskii, "On decomposition of plane figures in parts of least diameter" Colloq. Math. , 21 : 2 (1967) pp. 253–263 (In Russian)

References

[a1]	V.G. Boltyanskii, I.Ts. Gokhberg, "Sätze und Probleme der Kombinatorische Geometrie" , Deutsch. Verlag Wissenschaft. (1972) (Translated from Russian)