H-space

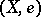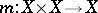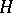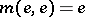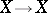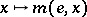A topological space with multiplication having a two-sided homotopy identity. More precisely, a pointed topological space for which a continuous mapping has been given is called an -space if and if the mappings , and are homotopic 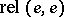to the identity mapping. The marked point is called the homotopy identity of the 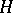-space 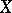. Sometimes the term "H-space" is used in a narrower sense: It is required that 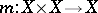be homotopy associative, i.e. that the mappings

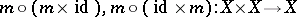are homotopic 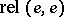. Sometimes one requires also the existence of a homotopy-inverse. This means that a mapping 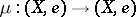must be given for which the mappings

are homotopic to the constant mapping 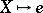. E.g., for any pointed topological space 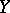the loop space 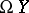is a homotopy-associative 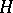-space with homotopy-inverse elements, while 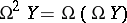is even a commutative 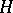-space, i.e. a space for which the mappings ,

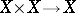are homotopic. The cohomology groups of an 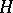-space form a Hopf algebra.

References

[1]	J.M. Boardman, R.M. Vogt, "Homotopy invariant algebraic structures on topological spaces" , Springer (1973)

Comments

Much of the importance of 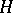-spaces (with the axioms of homotopy associativity and of homotopy inverse) comes from the fact that a group structure is induced on the set of homotopy classes of mappings from a space into an 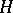-space. See [a1].

References

[a1]	E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. Chapt. I, Sect. 6