Fredholm mapping
For Banach spaces 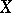 ,
, 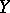 (cf. Banach space), let
(cf. Banach space), let 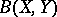 denote the set of bounded linear operators
denote the set of bounded linear operators 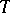 from
from 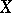 to
to 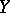 with domain
with domain  (cf. also Linear operator). An operator
(cf. also Linear operator). An operator 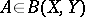 is called a Fredholm mapping if
is called a Fredholm mapping if
1) 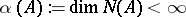 ;
;
2) 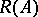 is closed in
is closed in 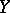 ;
;
3) 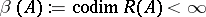 . Here,
. Here, 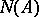 ,
, 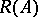 denote the null space and range of
denote the null space and range of 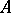 , respectively.
, respectively.
Properties.
Let 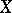 ,
,  ,
, 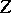 be Banach spaces. If
be Banach spaces. If 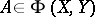 and
and 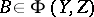 , then
, then 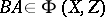 and
and
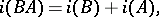 | (a1) |
where 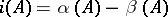 (the index). If
(the index). If 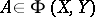 and
and 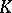 is a compact operator from
is a compact operator from 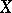 to
to 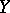 , then
, then 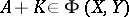 and
and
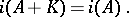 | (a2) |
Moreover, for each 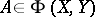 there is a
there is a 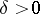 such that
such that 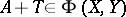 and
and
 | (a3) |
for each bounded mapping from 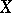 to
to 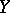 such that
such that 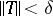 . If
. If 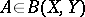 ,
, 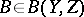 are such that
are such that 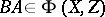 , then
, then 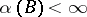 implies that
implies that 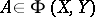 and
and 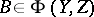 . The same is true if
. The same is true if  . If
. If 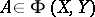 , then its adjoint operator
, then its adjoint operator 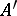 is in
is in 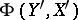 with
with 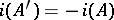 , where
, where 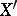 ,
, 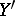 denote the dual spaces of
denote the dual spaces of 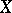 ,
, 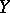 , respectively (cf. also Adjoint space).
, respectively (cf. also Adjoint space).
If 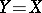 , it follows that
, it follows that 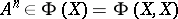 for each positive integer
for each positive integer  if
if 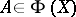 . Let
. Let
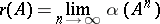 |
and
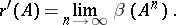 |
A necessary and sufficient condition for both 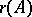 and
and 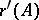 to be finite is that there exist an integer
to be finite is that there exist an integer  and operators
and operators 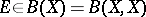 and
and 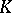 , compact on
, compact on 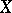 , such that
, such that 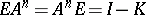 , where
, where 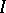 denotes the identity operator.
denotes the identity operator.
Semi-Fredholm operators.
Let 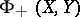 denote the set of all
denote the set of all 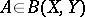 such that
such that 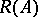 is closed in
is closed in  and
and  . Similarly,
. Similarly, 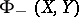 is the set of all
is the set of all 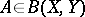 such that
such that 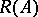 is closed in
is closed in 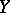 and
and 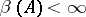 . If
. If 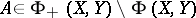 , then
, then 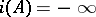 . If
. If 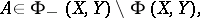 then
then 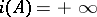 . If
. If 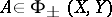 and
and 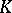 is compact from
is compact from 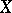 to
to 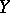 , then
, then 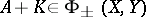 and
and 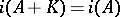 . If
. If 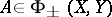 , then there is a
, then there is a 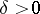 such that
such that 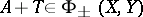 ,
, 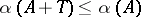 ,
, 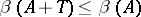 , and
, and 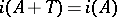 for any
for any 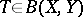 such that
such that  .
.
Non-linear Fredholm mappings.
Let 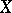 ,
, 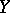 be Banach spaces, and let
be Banach spaces, and let  be an open connected subset of
be an open connected subset of 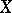 . A continuously Fréchet-differentiable mapping
. A continuously Fréchet-differentiable mapping 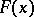 from
from  to
to 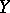 (cf. also Fréchet derivative) is Fredholm if
(cf. also Fréchet derivative) is Fredholm if 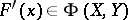 for each
for each 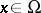 . Set
. Set  . It is independent of
. It is independent of  . If
. If 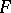 is a diffeomorphism, then
is a diffeomorphism, then 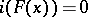 . If
. If 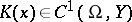 is a compact operator, then
is a compact operator, then  is Fredholm with
is Fredholm with  . A useful extension of the Sard theorem due to S. Smale [a2] states that if
. A useful extension of the Sard theorem due to S. Smale [a2] states that if 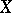 ,
, 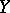 are separable (cf. also Separable space),
are separable (cf. also Separable space), 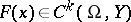 with
with 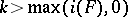 , then the critical values of
, then the critical values of 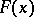 are nowhere dense in
are nowhere dense in 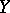 (cf. also Nowhere-dense set). It follows from this that if
(cf. also Nowhere-dense set). It follows from this that if 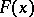 has negative index, then
has negative index, then 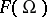 contains no interior points, i.e., if there is an
contains no interior points, i.e., if there is an 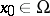 such that
such that  , then there are points
, then there are points 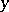 arbitrarily close to
arbitrarily close to 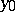 such that
such that 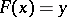 has no solution in
has no solution in  . Consequently, such equations are not considered well posed if
. Consequently, such equations are not considered well posed if 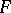 has negative index.
has negative index.
Perturbation theory.
The classes 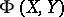 and
and 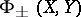 are stable under various types of perturbations. The set
are stable under various types of perturbations. The set 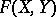 of Fredholm perturbations is the set of those
of Fredholm perturbations is the set of those 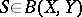 such that
such that 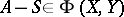 whenever
whenever 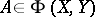 . The sets
. The sets 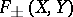 of semi-Fredholm perturbations are defined similarly. As noted, compact operators from
of semi-Fredholm perturbations are defined similarly. As noted, compact operators from 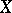 to
to 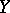 are in
are in 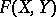 and
and 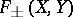 . So are strictly singular operators [a3] (in some spaces they may be non-compact). An operator
. So are strictly singular operators [a3] (in some spaces they may be non-compact). An operator 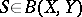 is in
is in 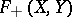 if and only if
if and only if 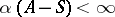 for all
for all 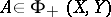 . Similarly, it is in
. Similarly, it is in 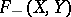 if and only if
if and only if 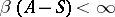 for all
for all 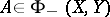 . But
. But 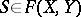 if and only if
if and only if 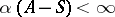 for all
for all 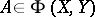 . On the other hand,
. On the other hand, 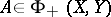 if and only if
if and only if 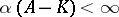 for all compact operators
for all compact operators 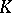 from
from 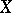 to
to 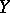 . Also,
. Also, 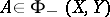 if and only if
if and only if 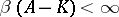 for all such
for all such 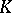 . Consequently,
. Consequently, 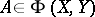 if and only if
if and only if 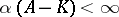 and
and  for all compact operators
for all compact operators  from
from 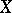 to
to 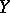 .
.
Perturbation functions.
There are several known "constants" that determine either the fact that a mapping is Fredholm or limit the size of arbitrary perturbations to keep the sum Fredholm. A well-known constant is due to T. Kato [a4]:
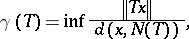 |
where the infimum is taken over those 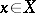 such that
such that 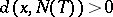 . If
. If 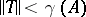 and
and 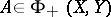 , then
, then 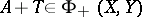 with (a3) holding. Other constants are:
with (a3) holding. Other constants are:
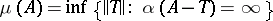 . A mapping
. A mapping 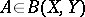 is in
is in 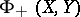 if and only if
if and only if 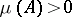 . Moreover, if
. Moreover, if 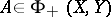 and
and 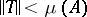 , then
, then 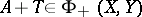 with (a3) holding.
with (a3) holding.
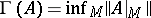 , where the infimum is taken over all infinite-dimensional subspaces
, where the infimum is taken over all infinite-dimensional subspaces 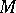 of
of 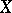 . A mapping
. A mapping 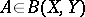 is in
is in  if and only if
if and only if 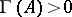 . Moreover,
. Moreover, 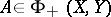 and
and 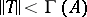 imply that
imply that 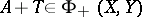 with (a3) holding.
with (a3) holding.
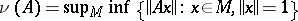 , where the supremum is taken over all subspaces
, where the supremum is taken over all subspaces 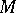 having finite codimension. If
having finite codimension. If 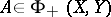 and
and  , then
, then 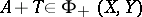 with (a3) holding as well.
with (a3) holding as well.
Unbounded Fredholm operators.
A linear operator 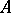 from
from  to
to 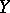 is called Fredholm if it is closed,
is called Fredholm if it is closed, 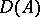 is dense in
is dense in 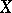 and
and 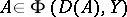 , where
, where 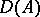 is considered a Banach space with norm
is considered a Banach space with norm 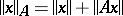 . Many of the facts that are true for bounded Fredholm mappings are true for such operators. In particular, the perturbation theorems hold. In fact, one can generalize them to include unbounded perturbations. A linear operator
. Many of the facts that are true for bounded Fredholm mappings are true for such operators. In particular, the perturbation theorems hold. In fact, one can generalize them to include unbounded perturbations. A linear operator 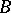 from
from 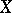 to
to 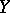 is called
is called 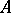 -compact if
-compact if 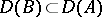 and for every sequence
and for every sequence 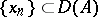 such that
such that 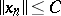 ,
, 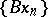 has a convergent subsequence. If
has a convergent subsequence. If 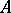 is Fredholm and
is Fredholm and 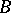 is
is 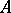 -compact, then
-compact, then 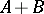 is Fredholm with the same index. A similar result holds when
is Fredholm with the same index. A similar result holds when 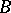 is
is 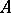 -bounded. Thus, if
-bounded. Thus, if 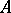 is Fredholm, then there is a
is Fredholm, then there is a 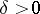 such that
such that 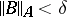 implies that
implies that 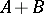 is Fredholm with (a3) holding for
is Fredholm with (a3) holding for 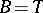 . If
. If 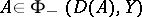 and
and  is a densely-defined closed operator from
is a densely-defined closed operator from 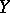 to
to 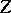 , then
, then 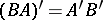 , where
, where 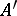 ,
, 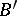 denote the conjugates of
denote the conjugates of 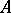 ,
,  , respectively (cf. also Adjoint operator).
, respectively (cf. also Adjoint operator).
References
| [a1] | I.C. Gohberg, M.G. Krein, "The basic propositions on defect numbers, root numbers and indices of linear operators" , Transl. Ser. 2 , 13 , Amer. Math. Soc. (1960) pp. 185–264 |
| [a2] | S. Smale, "An infinite dimensional version of Sard's theorem" Amer. J. Math. , 87 (1965) pp. 861–867 |
| [a3] | S. Goldberg, "Unbounded linear operators" , McGraw-Hill (1966) |
| [a4] | T. Kato, "Perturbation theory for linear operators" , Springer (1966) |
| [a5] | M. Schechter, "Basic theory of Fredholm operators" Ann. Scuola Norm. Sup. Pisa , 21 (1967) pp. 361–380 |
| [a6] | M. Schechter, "Riesz operators and Fredholm perturbations" Bull. Amer. Math. Soc. , 74 (1968) pp. 1139–1144 |
| [a7] | M. Schechter, "Principles of functional analysis" , Acad. Press (1971) |
| [a8] | M.S. Berger, "Nonlinearity and functional analysis" , Acad. Press (1977) |
Fredholm mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_mapping&oldid=18618