Comparison function
A function that is used in studying the character of growth of the modulus of an entire function 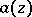 when
when 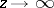 ; a comparison is normally made here between the behaviour of
; a comparison is normally made here between the behaviour of 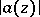 and that of a certain "good" entire function
and that of a certain "good" entire function  . Here naturally arises the problem of describing a sufficiently broad set of entire functions
. Here naturally arises the problem of describing a sufficiently broad set of entire functions  the elements of which could successfully be used as "comparison standards" .
the elements of which could successfully be used as "comparison standards" .
An entire function 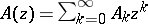 is called a comparison function, or
is called a comparison function, or 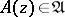 , if: 1)
, if: 1) 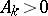 (
(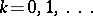 ); and 2)
); and 2) 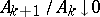 as
as 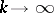 . An entire function
. An entire function 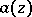 is called
is called  -comparable if there exists a constant
-comparable if there exists a constant  ,
, 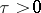 , such that
, such that
 | (1) |
The lower bound 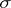 of the numbers
of the numbers 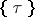 for which the relation (1) is fulfilled is called the
for which the relation (1) is fulfilled is called the 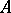 -type of the
-type of the  -comparable entire function
-comparable entire function 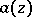 . The following theorem on
. The following theorem on 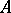 -types holds: If an entire function
-types holds: If an entire function 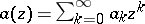 is comparable with
is comparable with 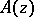 ,
, 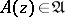 , then its
, then its 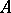 -type
-type 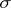 can be calculated using the formula
can be calculated using the formula
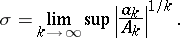 | (2) |
The given class 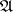 of comparison functions is known to give a complete solution of this problem, since for any entire function
of comparison functions is known to give a complete solution of this problem, since for any entire function 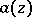 , other than a polynomial, there exists a comparison function
, other than a polynomial, there exists a comparison function 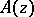 ,
,  , such that
, such that 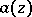 is comparable with
is comparable with 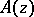 and such that its
and such that its 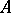 -type is equal to 1.
-type is equal to 1.
If an entire function  is comparable with
is comparable with 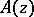 ,
,  , and its
, and its 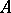 -type is equal to
-type is equal to 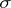 , then the function
, then the function
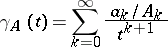 |
is analytic, according to (2), for 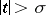 ; it is called
; it is called 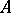 -associated with
-associated with 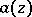 . In this case, the generalized Borel representation holds for
. In this case, the generalized Borel representation holds for 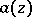 :
:
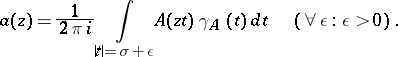 | (3) |
If 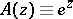 is taken as a comparison function, then (3) is the classical Borel integral representation of entire functions of exponential type
is taken as a comparison function, then (3) is the classical Borel integral representation of entire functions of exponential type 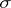 .
.
If 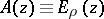 holds in (3), where
holds in (3), where 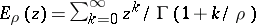 (
(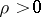 ) is a Mittag-Leffler function, then (3) is an integral representation for any entire function
) is a Mittag-Leffler function, then (3) is an integral representation for any entire function 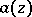 of order
of order 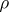 and of type
and of type 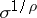 (
(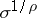 is the type of
is the type of 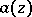 in the classical sense).
in the classical sense).
For certain cases of 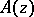 , an inverse transformation to (3) has been constructed (see, for example [1], which has a bibliography relating to comparison functions). Comparison functions and the Borel representation (3) are used in various questions of analysis (see, for example, [2], [3]). If
, an inverse transformation to (3) has been constructed (see, for example [1], which has a bibliography relating to comparison functions). Comparison functions and the Borel representation (3) are used in various questions of analysis (see, for example, [2], [3]). If 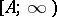 is the class of entire functions that are comparable with a given comparison function
is the class of entire functions that are comparable with a given comparison function 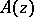 , then, for any sequence of comparison functions
, then, for any sequence of comparison functions  , there always exists an entire function
, there always exists an entire function 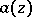 such that
such that 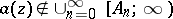 .
.
References
| [1] | R.P. Boas, R.C. Buck, "Polynomial expansions of analytic functions" , Springer & Acad. Press (U.S.A. & Canada) (1958) |
| [2] | M.M. Dzhrbashyan, "Integral transforms and representation of functions in the complex domain" , Moscow (1966) (In Russian) |
| [3] | Yu.A. Kaz'min, "A certain problem of A.O. Gel'fond" Math. USSR Sb. , 19 : 4 (1973) pp. 509–530 Mat. Sb. , 90 : 4 (1973) pp. 521–543 |
Comparison function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Comparison_function&oldid=18614