Golubev-Privalov theorem
If  is a complex summable function on a closed rectifiable Jordan curve
is a complex summable function on a closed rectifiable Jordan curve  in the complex
in the complex  -plane, then a necessary and sufficient condition for the existence of a function
-plane, then a necessary and sufficient condition for the existence of a function  , regular in the interior of the domain
, regular in the interior of the domain  bounded by
bounded by  and whose angular boundary values coincide with
and whose angular boundary values coincide with  almost-everywhere on
almost-everywhere on  , is
, is
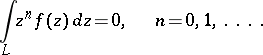 | (1) |
These conditions are known as the Golubev–Privalov conditions. That they are sufficient has been shown by V.V. Golubev [1]; that they are necessary has been shown by I.I. Privalov [2]. In other words, conditions (1) are necessary and sufficient for the integral of Cauchy–Lebesgue type (cf. Cauchy integral) 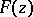 constructed for the function
constructed for the function 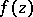 and the curve
and the curve  :
:
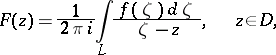 |
to be a Cauchy–Lebesgue integral.
In a more general formulation, let  be a complex Borel measure on
be a complex Borel measure on 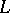 . Then the integral of Cauchy–Stieltjes type (cf. Cauchy integral),
. Then the integral of Cauchy–Stieltjes type (cf. Cauchy integral),
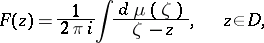 |
is a Cauchy–Stieltjes integral if and only if the generalized Golubev–Privalov conditions
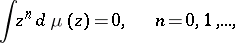 | (2) |
are satisfied.
In other words, conditions (2) are necessary and sufficient for the existence of a regular function  in
in  such that its angular boundary values coincide almost-everywhere (with respect to Lebesgue measure) on
such that its angular boundary values coincide almost-everywhere (with respect to Lebesgue measure) on 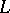 with
with
 |
where  is the angle between the positive direction of the abscissa axis and the tangent to
is the angle between the positive direction of the abscissa axis and the tangent to 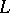 at the point
at the point 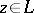 and
and 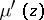 is the derivative of
is the derivative of  with respect to Lebesgue measure (arc length) on
with respect to Lebesgue measure (arc length) on 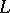 .
.
The Golubev–Privalov theorem is of importance in the theory of boundary properties of analytic functions.
References
| [1] | V.V. Golubev, "Univalent analytic functions with perfect sets of singular points" , Moscow (1916) (In Russian) (See also: V.V. Golubev, Single-valued analytic functions. Automorphic functions, Moscow, 1961 (in Russian)) |
| [2] | I.I. Privalov, "The Cauchy integral" , Saratov (1918) (In Russian) |
| [3] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
References
| [a1] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Golubev-Privalov theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Golubev-Privalov_theorem&oldid=18613