Measure
measure of a set
A notion that generalizes those of the length of segments, the area of figures and the volume of bodies, and that corresponds intuitively to the mass of a set for some mass distribution throughout the space. The notion of the measure of a set arose in the theory of functions of a real variable in connection with the study and improvement of the notion of an integral.
Definition and general properties.
Let 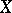 be a set and let
be a set and let 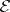 be a class of subsets of
be a class of subsets of 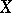 . A non-negative (not necessarily finite) set function
. A non-negative (not necessarily finite) set function 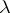 defined on
defined on 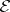 is called additive, finitely additive or countably additive if
is called additive, finitely additive or countably additive if
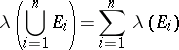 |
whenever
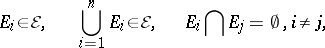 |
for, respectively, 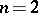 ,
,  arbitrary finite, and
arbitrary finite, and 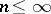 .
.
A collection 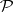 of subsets of
of subsets of 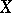 is called a semi-ring of sets if
is called a semi-ring of sets if
1) 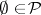 ;
;
2) 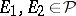 imply
imply 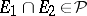 ;
;
3) 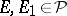 ,
, 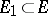 imply that
imply that 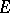 is representable as
is representable as 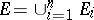 ,
, 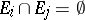 for
for 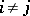 ,
, 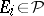 ,
, 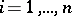 ,
, 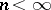 .
.
A collection 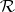 of subsets of
of subsets of 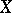 is called a ring of sets if
is called a ring of sets if
1) 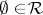 ;
;
2) 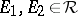 imply
imply 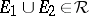 ,
, 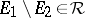 .
.
An example of a semi-ring is:  ,
, 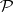 is the collection of all intervals of the form
is the collection of all intervals of the form
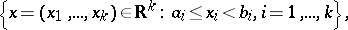 |
where 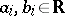 for
for 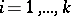 . The collection of all possible finite unions of such intervals is a ring.
. The collection of all possible finite unions of such intervals is a ring.
A collection 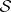 of subsets of
of subsets of 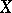 is called a
is called a 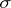 -ring if
-ring if
1) 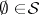 ;
;
2) 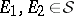 imply
imply 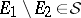 ;
;
3)  ,
, 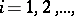 implies
implies 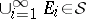 .
.
Every 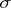 -ring is a ring; every ring is a semi-ring.
-ring is a ring; every ring is a semi-ring.
A finitely-additive measure is a non-negative finitely-additive set function 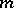 such that
such that 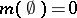 . The domain of definition
. The domain of definition 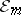 of a finitely-additive measure may be a semi-ring, a ring or a
of a finitely-additive measure may be a semi-ring, a ring or a 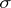 -ring. In the definition of a finitely-additive measure on a ring or on a
-ring. In the definition of a finitely-additive measure on a ring or on a 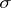 -ring the condition of finite additivity can be weakened to additivity, which leads to the same notion.
-ring the condition of finite additivity can be weakened to additivity, which leads to the same notion.
If 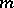 is a finitely-additive measure, if the sets
is a finitely-additive measure, if the sets 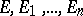 belong to its domain of definition, and if
belong to its domain of definition, and if 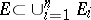 , then
, then
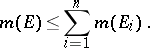 |
Let 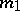 be a finitely-additive measure with domain
be a finitely-additive measure with domain 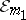 . A finitely-additive measure
. A finitely-additive measure 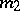 with domain
with domain 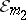 is called an extension of
is called an extension of 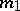 if
if 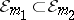 and
and 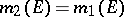 for all
for all 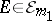 .
.
Every finitely-additive measure 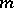 defined on a semi-ring
defined on a semi-ring 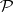 admits a unique extension to a finitely-additive measure
admits a unique extension to a finitely-additive measure 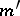 on the smallest ring
on the smallest ring 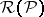 containing
containing 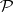 . This extension is defined as follows: Every
. This extension is defined as follows: Every 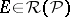 is representable as
is representable as 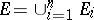 ,
, 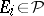 ,
, 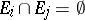 ,
, 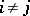 , and one sets
, and one sets
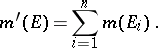 |
A finitely-additive measure that has the property of countable additivity is called a measure. Examples of measures: Let 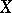 be an arbitrary non-empty set, let
be an arbitrary non-empty set, let 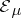 be a
be a 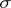 -ring, a ring or a semi-ring of subsets of
-ring, a ring or a semi-ring of subsets of 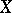 , let
, let 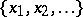 be a countable subset of
be a countable subset of 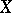 , and let
, and let 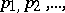 be non-negative numbers. Then the function
be non-negative numbers. Then the function
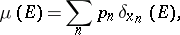 |
where 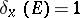 if
if  and
and 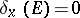 if
if 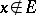 , is a measure defined on
, is a measure defined on 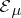 . The measures
. The measures 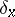 are called elementary, degenerate or Dirac measures (sometimes, Dirac masses). Not every finitely-additive measure is a measure. For example, if
are called elementary, degenerate or Dirac measures (sometimes, Dirac masses). Not every finitely-additive measure is a measure. For example, if 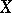 is the set of rational points of the segment
is the set of rational points of the segment 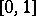 ,
, 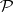 is the semi-ring of all possible intersections of subintervals of
is the semi-ring of all possible intersections of subintervals of 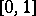 with
with 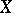 , and for every
, and for every 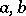 ,
, 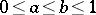 ,
,
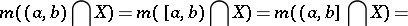 |
 |
then 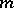 is finitely additive, but not countably additive on
is finitely additive, but not countably additive on 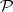 .
.
A (finitely-additive) measure 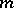 with domain
with domain 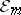 is said to be finite (respectively,
is said to be finite (respectively, 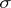 -finite) if
-finite) if 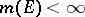 for all
for all 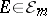 (respectively, if for every
(respectively, if for every 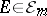 there is a sequence of sets
there is a sequence of sets 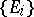 in
in 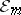 such that
such that 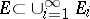 and
and 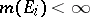 ,
,  ). A (finitely-additive) measure
). A (finitely-additive) measure 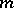 is said to be totally finite (totally
is said to be totally finite (totally 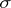 -finite) if it is finite (respectively,
-finite) if it is finite (respectively, 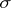 -finite) and
-finite) and 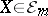 .
.
A pair 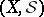 , where
, where 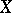 is a set and
is a set and 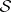 is a
is a 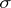 -ring of subsets of
-ring of subsets of 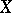 such that
such that 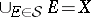 , is called a measurable space. A triple
, is called a measurable space. A triple 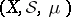 , where
, where 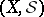 is a measurable space and
is a measurable space and 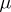 is a measure on
is a measure on 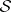 , is called a measure space. A space with a totally-finite measure
, is called a measure space. A space with a totally-finite measure 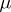 normalized by the condition
normalized by the condition 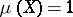 is called a probability space. In abstract measure theory, where the basic notions are a measurable space
is called a probability space. In abstract measure theory, where the basic notions are a measurable space 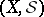 or a measure space
or a measure space 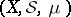 , the elements of
, the elements of 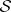 are also referred to as measurable sets (cf. also Measurable set).
are also referred to as measurable sets (cf. also Measurable set).
Properties of measure spaces.
Let 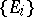 be an arbitrary sequence of measurable sets. Then
be an arbitrary sequence of measurable sets. Then
1) 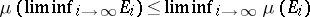 ;
;
2) if 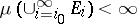 for some
for some 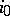 , then
, then
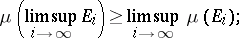 |
3) if 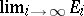 exists and the condition in 2) is satisfied, then
exists and the condition in 2) is satisfied, then
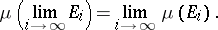 |
A finitely-additive measure 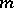 defined on a ring
defined on a ring 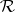 is a measure if and only if
is a measure if and only if
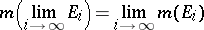 |
for every monotone increasing sequence 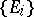 of elements of
of elements of 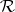 such that
such that 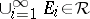 .
.
Let 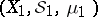 be a measure space, let
be a measure space, let 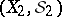 be a measurable space and let
be a measurable space and let 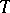 be a measurable mapping from
be a measurable mapping from 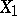 into
into 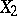 , i.e.
, i.e.
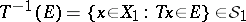 |
for all 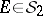 . The measure generated by the mapping
. The measure generated by the mapping 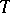 (denoted here by
(denoted here by 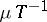 ) is the measure on
) is the measure on 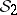 defined by
defined by
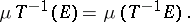 |
Let 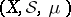 be a measure space and let
be a measure space and let 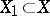 . Define
. Define 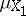 on the sets
on the sets 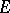 from the
from the  -ring
-ring 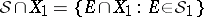 by
by
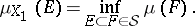 |
Then 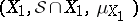 is a measure space;
is a measure space; 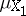 is called the restriction of the measure
is called the restriction of the measure 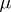 to
to 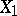 .
.
An atom of the space 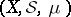 (or of the measure
(or of the measure 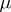 ) is any set
) is any set 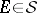 of positive measure such that if
of positive measure such that if 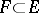 ,
, 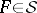 , then either
, then either 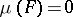 or
or 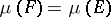 . A measure space without atoms is called non-atomic or continuous (in this case
. A measure space without atoms is called non-atomic or continuous (in this case 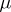 is also called non-atomic or continuous). If
is also called non-atomic or continuous). If 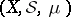 is a space with a non-atomic
is a space with a non-atomic 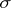 -finite measure and
-finite measure and 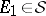 , then for every
, then for every 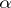 with
with 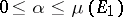 (possibly
(possibly 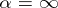 ) there is an element
) there is an element 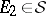 such that
such that 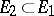 and
and 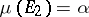 .
.
A measure space 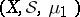 (or the measure
(or the measure 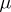 ) is said to be complete if
) is said to be complete if 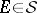 ,
, 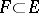 ,
, 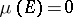 imply
imply 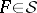 . Every measure space
. Every measure space 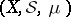 can be completed by adjoining to
can be completed by adjoining to 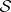 all the sets of the form
all the sets of the form 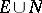 with
with 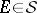 ,
, 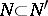 ,
, 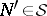 ,
, 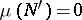 , and putting for such sets
, and putting for such sets 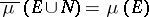 . The class of sets of the indicated form is a
. The class of sets of the indicated form is a 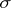 -ring, and
-ring, and 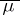 is a complete measure on it. The sets of null measure are called null sets. If the set of points of
is a complete measure on it. The sets of null measure are called null sets. If the set of points of 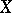 at which a property
at which a property 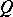 is not satisfied is a null set, then property
is not satisfied is a null set, then property 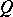 is said to hold almost-everywhere.
is said to hold almost-everywhere.
Extension of measures.
A measure 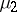 is an extension of a measure
is an extension of a measure 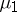 if
if 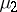 is an extension of
is an extension of 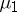 in the class of finitely-additive measures (see above). Every measure defined on a semi-ring
in the class of finitely-additive measures (see above). Every measure defined on a semi-ring 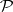 admits a unique extension to a measure on the ring
admits a unique extension to a measure on the ring 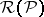 generated by
generated by 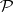 (the extension is realized in the same way as in the case of finitely-additive measures). Further, every measure
(the extension is realized in the same way as in the case of finitely-additive measures). Further, every measure  defined on a ring
defined on a ring 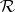 can be extended to a measure
can be extended to a measure 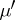 on the
on the 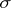 -ring
-ring 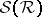 generated by
generated by 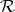 ; if
; if  is
is 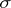 -finite, then
-finite, then 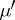 is unique and
is unique and 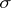 -finite. The value of
-finite. The value of 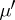 on any set
on any set 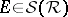 can be given by the formula
can be given by the formula
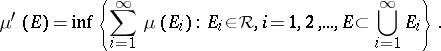 | (*) |
A class of subsets of 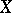 is called hereditary if it contains, together with any set in the class, all its subsets. An outer measure is a set function
is called hereditary if it contains, together with any set in the class, all its subsets. An outer measure is a set function 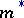 , defined on a hereditary
, defined on a hereditary 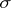 -ring
-ring 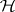 (i.e. a class of sets which is simultaneously hereditary and a
(i.e. a class of sets which is simultaneously hereditary and a 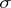 -ring), which has the following properties:
-ring), which has the following properties:
1) 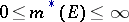 ,
, 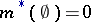 ;
;
2) 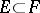 implies
implies 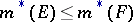 ;
;
3) 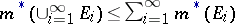 .
.
Given a measure 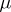 on the ring
on the ring 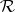 one can construct an outer measure
one can construct an outer measure 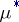 on the hereditary
on the hereditary 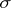 -ring
-ring 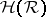 generated by
generated by 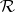 (
(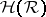 consists of all sets that can be covered by a countable union of elements of
consists of all sets that can be covered by a countable union of elements of 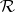 ) by means of the formula
) by means of the formula
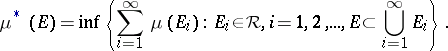 |
The outer measure 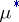 is called the outer measure induced by the measure
is called the outer measure induced by the measure 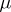 .
.
Let 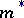 be an outer measure on a hereditary
be an outer measure on a hereditary 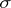 -ring
-ring 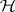 of subsets of
of subsets of 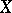 . A set
. A set 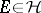 is called
is called 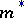 -measurable if
-measurable if
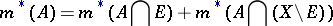 |
for every 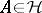 . The collection
. The collection 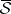 of
of 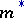 -measurable sets is a
-measurable sets is a 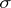 -ring which contains all sets of null outer measure. The set function
-ring which contains all sets of null outer measure. The set function 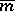 on
on 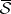 defined by the equality
defined by the equality 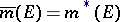 is a complete measure and is called the measure induced by the outer measure
is a complete measure and is called the measure induced by the outer measure 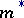 .
.
Suppose that 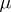 is a measure on a ring
is a measure on a ring 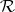 and that
and that 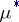 is the outer measure on
is the outer measure on 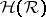 induced by
induced by 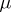 . Let
. Let 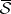 and
and 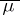 denote the collection of
denote the collection of 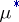 -measurable sets and the measure on
-measurable sets and the measure on 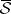 induced by
induced by 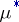 , respectively. Then
, respectively. Then 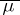 is an extension of
is an extension of 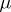 , and since
, and since 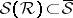 it follows that the function
it follows that the function 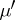 on
on 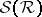 given by formula (*) is also a measure extending
given by formula (*) is also a measure extending  . If the original measure
. If the original measure 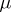 on
on 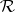 is
is 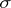 -finite, then the space
-finite, then the space 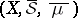 is the completion of the space
is the completion of the space 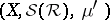 (see (*)). If
(see (*)). If 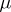 is given on the
is given on the 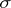 -ring
-ring 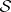 , then the induced outer measure
, then the induced outer measure 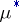 on the hereditary
on the hereditary 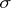 -ring
-ring 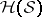 generated by
generated by 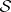 is given by the formula
is given by the formula
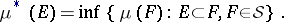 |
Alongside with the outer measure 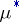 , one defines the inner measure induced by the measure
, one defines the inner measure induced by the measure 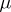 on
on 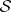 . It is defined as
. It is defined as
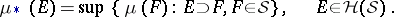 |
For every set 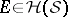 a measurable kernel
a measurable kernel 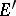 and a measurable envelope
and a measurable envelope 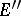 are defined as elements of
are defined as elements of 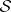 such that
such that 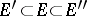 and
and 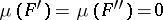 for all
for all 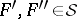 such that
such that 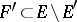 ,
, 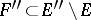 . A measurable kernel exists always, while a measurable envelope exists whenever
. A measurable kernel exists always, while a measurable envelope exists whenever 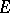 has
has 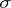 -finite outer measure; moreover,
-finite outer measure; moreover, 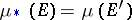 and
and 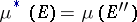 . Let
. Let 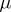 be a measure on a ring
be a measure on a ring 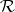 and let
and let 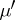 be its extension to the
be its extension to the  -ring
-ring 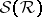 generated by
generated by 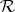 . The inner measure
. The inner measure 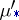 on the subsets
on the subsets 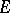 of finite
of finite 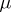 -measure can be expressed in terms of the outer measure
-measure can be expressed in terms of the outer measure 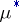 (and hence
(and hence 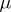 ):
):
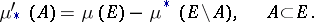 |
Furthermore, a set 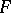 belonging to the hereditary
belonging to the hereditary 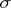 -ring
-ring 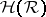 with finite outer
with finite outer 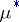 -measure is
-measure is 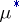 -measurable if and only if
-measurable if and only if 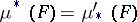 . In case the original measure
. In case the original measure 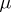 on
on 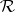 is totally finite, one has the following necessary and sufficient condition for the
is totally finite, one has the following necessary and sufficient condition for the 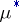 -measurability of a set
-measurability of a set 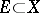 :
:
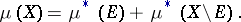 |
For totally-finite measures on 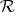 this condition is frequently taken as the definition of
this condition is frequently taken as the definition of 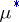 -measurability of the set
-measurability of the set 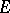 .
.
If 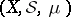 is a space with a
is a space with a 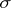 -finite measure and
-finite measure and 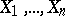 is a finite collection of elements of the hereditary
is a finite collection of elements of the hereditary 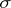 -ring
-ring 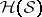 generated by
generated by 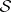 , then on the
, then on the 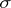 -ring
-ring 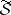 generated by
generated by 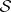 and the sets
and the sets 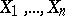 one can define a measure
one can define a measure 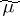 which agrees with
which agrees with 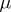 on
on 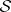 .
.
Jordan, Lebesgue and Lebesgue–Stieltjes measures.
An example of an extension of a measure is provided by the Lebesgue measure in 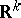 . The intervals of the form
. The intervals of the form
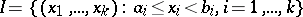 |
form a semi-ring 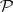 in
in 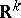 . For each such interval, let
. For each such interval, let
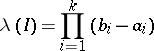 |
(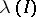 coincides with the volume of
coincides with the volume of 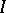 ). The function
). The function 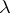 is
is 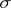 -finite and countably additive on
-finite and countably additive on 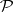 and admits a unique extension to a measure
and admits a unique extension to a measure 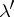 on the
on the 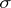 -ring
-ring 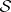 generated by
generated by 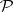 ;
; 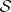 is identical with the
is identical with the 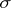 -ring of Borel sets (cf. Borel set) (or Borel-measurable sets) in
-ring of Borel sets (cf. Borel set) (or Borel-measurable sets) in 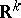 . The measure
. The measure 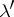 was first defined by E. Borel in 1898 (see Borel measure). The completion
was first defined by E. Borel in 1898 (see Borel measure). The completion 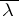 of
of 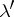 (defined on
(defined on 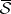 ) is called the Lebesgue measure, and was introduced by H. Lebesgue in 1902 (see Lebesgue measure). A set belonging to the domain
) is called the Lebesgue measure, and was introduced by H. Lebesgue in 1902 (see Lebesgue measure). A set belonging to the domain 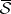 of
of 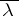 is called Lebesgue measurable. A bounded set
is called Lebesgue measurable. A bounded set 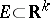 belongs to
belongs to 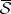 if and only if
if and only if 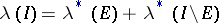 , where
, where 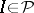 is some interval containing
is some interval containing 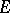 ; in this case
; in this case 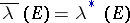 . A set
. A set 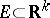 belongs to
belongs to 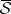 if and only if for some sequence
if and only if for some sequence 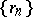 ,
, 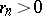 ,
, 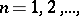 such that
such that 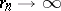 , one has
, one has 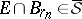 for all
for all  , where
, where 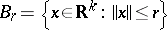 . The cardinality of the family of all Borel sets in
. The cardinality of the family of all Borel sets in 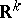 is
is  (the cardinality of the continuum), whereas the cardinality of the family of all Lebesgue-measurable sets is
(the cardinality of the continuum), whereas the cardinality of the family of all Lebesgue-measurable sets is 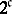 , so that the inclusion
, so that the inclusion 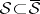 is strict, i.e. there exist Lebesgue-measurable sets that are not Borel measurable.
is strict, i.e. there exist Lebesgue-measurable sets that are not Borel measurable.
The Lebesgue measure 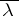 is invariant under linear orthogonal transformations
is invariant under linear orthogonal transformations 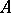 of
of 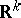 as well as under translations by elements
as well as under translations by elements 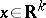 , i.e.
, i.e. 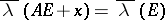 for all
for all 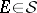 .
.
Using the axiom of choice one can show that there exist sets which are not Lebesgue measurable. On the straight line, for example, such a set can be obtained by picking one point in each coset in 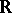 of the additive subgroup of rational numbers (Vitali's example).
of the additive subgroup of rational numbers (Vitali's example).
Historically the Borel and Lebesgue measures in 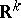 were preceded by the measure defined by C. Jordan in 1892 (see Jordan measure). The idea of the definition of the Jordan measure is very close to that of the classic definition of area and volume, which goes back to ancient Greece. Thus, a set
were preceded by the measure defined by C. Jordan in 1892 (see Jordan measure). The idea of the definition of the Jordan measure is very close to that of the classic definition of area and volume, which goes back to ancient Greece. Thus, a set 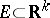 is called Jordan measurable if there exist two sets, representable as finite unions of disjoint rectangles, one contained in
is called Jordan measurable if there exist two sets, representable as finite unions of disjoint rectangles, one contained in 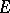 and the other containing
and the other containing 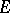 , such that the difference of their volumes (defined in an obvious manner) is arbitrarily small. The Jordan measure of such a set is the infimum of the volumes of finite unions of rectangles covering
, such that the difference of their volumes (defined in an obvious manner) is arbitrarily small. The Jordan measure of such a set is the infimum of the volumes of finite unions of rectangles covering 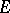 . A Jordan-measurable set is also Lebesgue measurable, and its Jordan and Lebesgue measures are equal. The domain of the Jordan measure is merely a ring, and not a
. A Jordan-measurable set is also Lebesgue measurable, and its Jordan and Lebesgue measures are equal. The domain of the Jordan measure is merely a ring, and not a 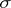 -ring, which restricts considerably its domain of applicability.
-ring, which restricts considerably its domain of applicability.
The Lebesgue measure is a particular case of the more general Lebesgue–Stieltjes measure. The latter is defined by means of a real-valued function 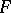 on
on 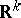 with the properties:
with the properties:
1) 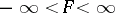 ;
;
2) 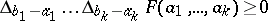 for
for 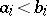 ,
, 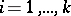 , where
, where 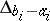 is the difference operator with step
is the difference operator with step 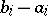 taken at the point
taken at the point 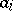 with respect to the
with respect to the 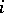 -th coordinate;
-th coordinate;
3) 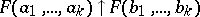 as
as 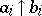 ,
, 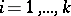 .
.
Given such a function 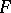 , the measure
, the measure 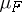 of the interval
of the interval
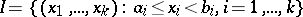 |
is defined by the formula
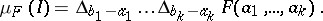 |
It turns out that 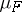 is countably additive on the semi-ring of all such intervals and that it admits an extension to the
is countably additive on the semi-ring of all such intervals and that it admits an extension to the 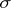 -algebra of Borel sets; the completion of this extension yields what is called the Lebesgue–Stieltjes measure corresponding to
-algebra of Borel sets; the completion of this extension yields what is called the Lebesgue–Stieltjes measure corresponding to 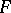 . For the particular choice
. For the particular choice
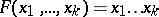 |
one obtains the Lebesgue measure.
Measures in product spaces.
By definition, the product of two measurable spaces 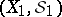 ,
, 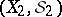 is the measurable space consisting of the set
is the measurable space consisting of the set 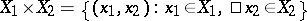 (the product of
(the product of 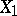 and
and 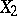 ) and the
) and the  -ring
-ring 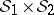 of subsets of
of subsets of 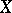 (the product of the
(the product of the  -rings
-rings 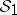 and
and 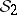 ) generated by the semi-ring
) generated by the semi-ring 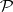 of sets of the form
of sets of the form
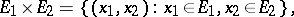 |
where 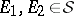 . If
. If 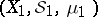 and
and 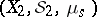 are measure spaces, the formula
are measure spaces, the formula
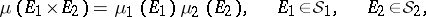 |
defines a measure on 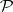 ; if
; if 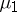 and
and 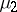 are
are 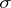 -finite,
-finite, 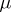 extends uniquely to a measure on
extends uniquely to a measure on 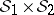 , denoted by
, denoted by 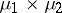 . The measure
. The measure 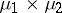 and the space
and the space 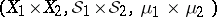 are called, respectively, the product of the measures
are called, respectively, the product of the measures 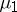 and
and 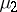 , and the product of the measure spaces
, and the product of the measure spaces 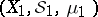 and
and 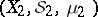 . The completion of the product of the Lebesgue measure in
. The completion of the product of the Lebesgue measure in 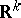 and the Lebesgue measure in
and the Lebesgue measure in 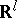 is the Lebesgue measure in
is the Lebesgue measure in 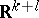 . Analogously one defines the product of an arbitrary finite number of measure spaces.
. Analogously one defines the product of an arbitrary finite number of measure spaces.
Let 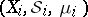 ,
, 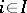 , be an arbitrary family of measure spaces such that
, be an arbitrary family of measure spaces such that 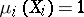 ,
, 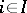 . The product space
. The product space 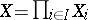 is, by definition, the set of all functions on
is, by definition, the set of all functions on 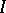 such that the value at each
such that the value at each 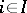 is an element
is an element 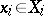 . A measurable rectangle in
. A measurable rectangle in 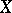 is any set of the form
is any set of the form 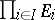 , where
, where 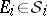 and only finitely many sets
and only finitely many sets 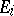 are different from
are different from 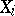 . The family of measurable rectangles forms a semi-ring
. The family of measurable rectangles forms a semi-ring 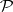 . The
. The 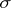 -ring generated by
-ring generated by 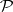 is denoted by
is denoted by 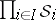 and is called the product of the
and is called the product of the 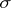 -rings
-rings 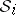 . Now, let
. Now, let 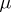 be the function on
be the function on 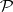 defined by
defined by 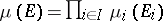 for
for 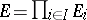 . The function
. The function 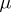 thus defined is a measure which admits a unique extension to a measure on
thus defined is a measure which admits a unique extension to a measure on 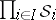 , denoted by
, denoted by 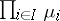 . The measure space
. The measure space 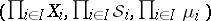 is called the product of the spaces
is called the product of the spaces 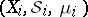 ,
, 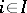 .
.
The product of an arbitrary number of measure spaces is a particular case of the following, more general, scheme, which plays an important role in probability theory. Let 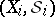 ,
, 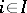 , be a family of measurable spaces (each
, be a family of measurable spaces (each 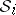 is a
is a 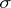 -algebra), and suppose that for each finite subset
-algebra), and suppose that for each finite subset 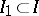 there is given a probability measure
there is given a probability measure 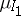 on the measurable spaces
on the measurable spaces 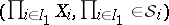 (the product of measures corresponds to the case that
(the product of measures corresponds to the case that 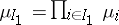 for all finite
for all finite 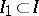 ). Suppose further that each two measures
). Suppose further that each two measures 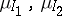 are compatible in the sense that if
are compatible in the sense that if 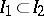 and
and 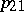 is the projection of
is the projection of 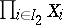 onto
onto 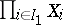 , then
, then 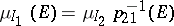 for all
for all 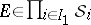 (by definition,
(by definition, 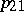 is the mapping of
is the mapping of 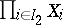 onto
onto 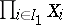 such that
such that 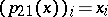 for all
for all 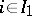 ). The following question arises: Is there a probability measure on
). The following question arises: Is there a probability measure on 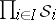 such that
such that 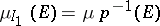 for every finite
for every finite 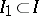 and every
and every 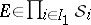 , where
, where 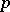 denotes the projection of
denotes the projection of 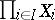 onto
onto 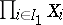 ? It turns out that such a measure does not always exist, and additional conditions must be imposed to guarantee its existence. One such condition is perfectness of the measures
? It turns out that such a measure does not always exist, and additional conditions must be imposed to guarantee its existence. One such condition is perfectness of the measures 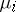 (corresponding to the one-point sets
(corresponding to the one-point sets 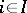 ). The notion of a perfect measure was first introduced by B.V. Gnedenko and A.N. Kolmogorov [6]. A space
). The notion of a perfect measure was first introduced by B.V. Gnedenko and A.N. Kolmogorov [6]. A space 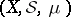 with a totally-finite measure, as well as the measure
with a totally-finite measure, as well as the measure 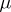 itself, is called perfect if for every
itself, is called perfect if for every 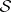 -measurable real-valued function
-measurable real-valued function 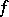 on
on 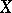 there is a Borel set
there is a Borel set 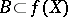 such that
such that 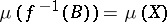 . The perfectness assumption eliminates a series of "pathological" phenomena that arise in general measure theory.
. The perfectness assumption eliminates a series of "pathological" phenomena that arise in general measure theory.
Measures in topological spaces.
The study of measures in topological spaces is usually concerned with measures defined on sets connected in some way or another with the topology of the underlying space. One of the typical approaches is the following. Let 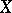 be an arbitrary topological space and let
be an arbitrary topological space and let 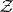 be the class of subsets of the form
be the class of subsets of the form 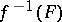 , where
, where 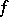 is a continuous real-valued function on
is a continuous real-valued function on 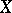 and
and 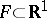 is a closed set. Let
is a closed set. Let 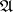 be the algebra generated by the class
be the algebra generated by the class 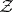 and let
and let 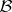 be the
be the 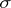 -algebra generated by
-algebra generated by 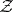 (
(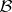 is called the
is called the 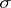 -algebra of Baire sets, cf. also Algebra of sets). Now let
-algebra of Baire sets, cf. also Algebra of sets). Now let 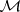 be the class of totally-finite finitely-additive measures
be the class of totally-finite finitely-additive measures 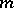 on
on 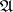 that are regular in the sense that
that are regular in the sense that
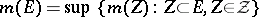 |
for all 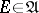 . In
. In 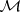 one distinguishes the subclasses
one distinguishes the subclasses 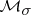 ,
, 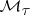 and
and 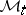 formed by the (finitely-additive) measures possessing additional smoothness properties. By definition,
formed by the (finitely-additive) measures possessing additional smoothness properties. By definition, 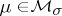 if
if 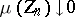 for every sequence
for every sequence 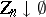 ,
, 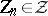 (this property is equivalent to the countable additivity of
(this property is equivalent to the countable additivity of 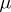 ; the measures from
; the measures from 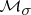 admit unique extensions to
admit unique extensions to 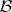 and hereafter it is assumed that they are given on
and hereafter it is assumed that they are given on 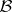 );
); 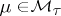 if
if 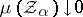 for every net
for every net 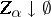 ,
, 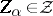 ; and
; and 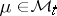 if for every
if for every 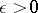 there is a compact set
there is a compact set 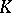 such that
such that 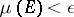 whenever
whenever 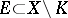 ,
, 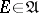 .
.
The inclusions 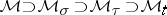 hold. The elements of
hold. The elements of 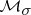 are called Baire measures.
are called Baire measures.
There is an intimate connection between the measures belonging to 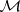 and the linear functionals on the space
and the linear functionals on the space 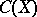 of bounded continuous functions on
of bounded continuous functions on 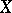 . Namely, the formula
. Namely, the formula
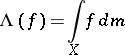 |
establishes a one-to-one correspondence between the finitely-additive measures 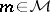 and the non-negative linear functionals
and the non-negative linear functionals 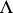 on
on 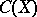 (non-negative means that
(non-negative means that 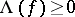 whenever
whenever 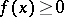 ,
, 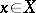 ). Moreover, for every set
). Moreover, for every set 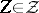 ,
,
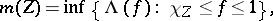 |
where 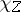 is the indicator function of
is the indicator function of 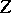 . This correspondence takes the measures from
. This correspondence takes the measures from 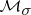 into
into 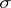 -smooth functionals
-smooth functionals 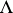 (i.e. functionals
(i.e. functionals 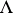 with the property that
with the property that 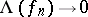 if
if 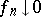 in
in 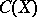 ), the measures from
), the measures from 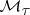 into
into  -smooth functionals
-smooth functionals 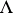 (i.e. functionals such that
(i.e. functionals such that 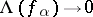 for every net
for every net 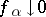 in
in 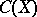 ), and the measures from
), and the measures from 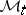 into dense functionals
into dense functionals 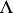 (i.e. with the property that
(i.e. with the property that 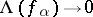 for every net
for every net 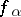 in
in 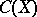 such that
such that 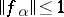 for all
for all  and
and 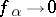 uniformly on compact subsets; here
uniformly on compact subsets; here  is the uniform norm).
is the uniform norm).
The space 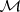 is usually endowed with the weak topology
is usually endowed with the weak topology 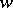 , in which a basis of neighbourhoods consists of the sets of the form
, in which a basis of neighbourhoods consists of the sets of the form
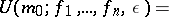 |
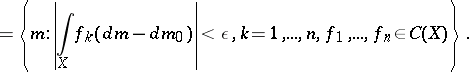 |
With the topology 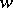 ,
, 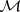 is a completely-regular Hausdorff space. Convergence in the topology
is a completely-regular Hausdorff space. Convergence in the topology 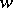 is usually denoted by the symbol
is usually denoted by the symbol 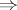 . For the convergence of a net
. For the convergence of a net 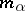 to
to 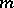 :
: 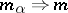 , it is necessary and sufficient that
, it is necessary and sufficient that 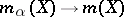 and
and 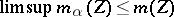 for all
for all 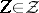 . Another necessary and sufficient condition for the convergence
. Another necessary and sufficient condition for the convergence 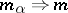 is that
is that 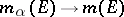 for all
for all 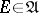 such that there are
such that there are 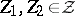 with
with 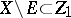 ,
, 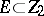 , and
, and 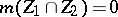 . If the space
. If the space 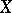 is completely regular and Hausdorff, then
is completely regular and Hausdorff, then 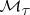 is metrizable if and only if
is metrizable if and only if 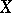 is metrizable. If
is metrizable. If 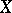 is metrizable, then
is metrizable, then 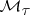 admits a metric in which it is separable if and only if
admits a metric in which it is separable if and only if 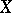 is separable, and it admits a metric in which it is complete if and only if
is separable, and it admits a metric in which it is complete if and only if 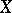 has a complete metric. If
has a complete metric. If 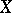 is metrizable, then
is metrizable, then 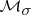 is metrizable if and only if it is metrizable by the Lévy–Prokhorov metric.
is metrizable if and only if it is metrizable by the Lévy–Prokhorov metric.
The space 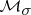 is sequentially closed in
is sequentially closed in  (Aleksandrov's theorem). A set
(Aleksandrov's theorem). A set 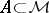 is called tight if
is called tight if 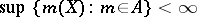 and if for every
and if for every 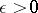 there is a compact set
there is a compact set 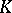 such that
such that 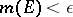 for all
for all 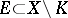 ,
, 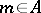 and
and 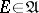 . If
. If 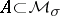 is tight, then
is tight, then 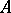 is relatively compact in
is relatively compact in 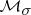 ; conversely, if
; conversely, if 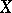 is metrizable and topologically complete, then
is metrizable and topologically complete, then 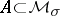 is relatively compact, and if every measure in
is relatively compact, and if every measure in 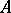 is concentrated on some separable subset of
is concentrated on some separable subset of 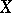 , then
, then 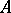 is tight (Prokhorov's theorem).
is tight (Prokhorov's theorem).
Under certain conditions the elements of 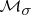 can be extended to Borel measures, i.e. measures defined on the
can be extended to Borel measures, i.e. measures defined on the 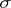 -algebra of Borel sets (see Borel set; Borel measure). For example, if
-algebra of Borel sets (see Borel set; Borel measure). For example, if 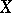 is a normal countably-paracompact Hausdorff space, then every measure
is a normal countably-paracompact Hausdorff space, then every measure 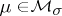 admits a unique extension to a regular Borel measure. If
admits a unique extension to a regular Borel measure. If 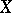 is completely regular and Hausdorff, then every
is completely regular and Hausdorff, then every  -smooth (tight) Baire measure admits a unique extension to a
-smooth (tight) Baire measure admits a unique extension to a  -smooth (tight) Borel measure.
-smooth (tight) Borel measure.
The support of a Baire (Borel) measure is the smallest set 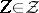 (respectively, the smallest closed set) the measure of which is equal to the measure of the whole space. Every
(respectively, the smallest closed set) the measure of which is equal to the measure of the whole space. Every  -smooth measure has a support.
-smooth measure has a support.
Often, when measures in topological spaces (especially in locally compact Hausdorff spaces) are considered, it is assumed that the Borel and Baire measures are given on less-wide classes of sets, more precisely — on 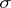 -rings generated by compact sets and, respectively, compact
-rings generated by compact sets and, respectively, compact 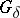 -sets.
-sets.
Let 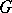 be a locally compact Hausdorff topological group. A left Haar measure on
be a locally compact Hausdorff topological group. A left Haar measure on 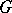 is a measure defined on the
is a measure defined on the  -ring generated by all compact subsets that does not vanish identically and is such that
-ring generated by all compact subsets that does not vanish identically and is such that 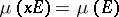 for all
for all 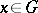 and
and 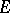 in the domain of
in the domain of 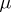 . A right Haar measure is defined in the same manner but with the condition
. A right Haar measure is defined in the same manner but with the condition 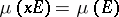 replaced by
replaced by 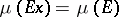 . On any group of the type considered a left Haar measure exists and is unique (up to a multiplicative positive constant). Every left Haar measure is regular in the sense that
. On any group of the type considered a left Haar measure exists and is unique (up to a multiplicative positive constant). Every left Haar measure is regular in the sense that 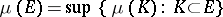 , where
, where 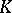 are compact sets. The right Haar measure has analogous properties. The Lebesgue measure on
are compact sets. The right Haar measure has analogous properties. The Lebesgue measure on 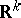 is a particular case of the Haar measure. See also Measure in a topological vector space.
is a particular case of the Haar measure. See also Measure in a topological vector space.
Isomorphism of measure spaces.
Let 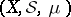 be a measure space. Call two sets
be a measure space. Call two sets 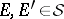
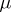 -equal (written
-equal (written 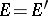
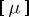 ) if
) if 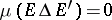 (where
(where 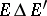 denotes the symmetric difference of
denotes the symmetric difference of 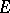 and
and 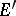 , cf. Symmetric difference of sets). Denote by
, cf. Symmetric difference of sets). Denote by  the class of sets
the class of sets 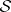 with this equality relation. In
with this equality relation. In 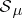 the set-theoretic operations, performed a finite (or countable) number of times are correctly defined: for example, if
the set-theoretic operations, performed a finite (or countable) number of times are correctly defined: for example, if 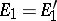
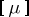 and
and 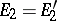
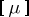 , then
, then 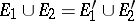
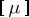 . The measure
. The measure 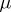 is carried over, in an obvious manner, to
is carried over, in an obvious manner, to 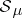 .
.
Let 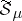 be the subset of
be the subset of 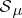 consisting of the sets of finite measure. The function
consisting of the sets of finite measure. The function 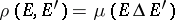 on
on 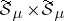 is a metric. The measure space
is a metric. The measure space 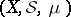 is said to be separable if the space
is said to be separable if the space 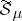 with metric
with metric 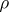 is separable. If
is separable. If 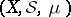 is a space with a
is a space with a 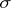 -finite measure and the
-finite measure and the 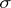 -ring
-ring 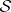 is countably generated (i.e. there is a countable family
is countably generated (i.e. there is a countable family 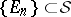 such that
such that 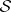 is the smallest
is the smallest 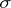 -ring that contains this family), then the metric space
-ring that contains this family), then the metric space 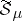 is separable.
is separable.
Two measure spaces, 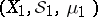 and
and 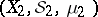 are said to be isomorphic if there is a one-to-one mapping
are said to be isomorphic if there is a one-to-one mapping  of
of 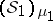 onto
onto 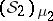 such that
such that
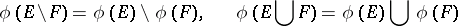 |
and
 |
Now, let 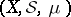 be an arbitrary space with a totally-finite measure. There is a partition of
be an arbitrary space with a totally-finite measure. There is a partition of 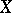 into disjoint sets
into disjoint sets 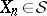 ,
,  such that the restriction of
such that the restriction of 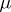 to
to  is isomorphic either to a measure concentrated at one point or to a measure which is equal, up to a positive factor, to the direct product
is isomorphic either to a measure concentrated at one point or to a measure which is equal, up to a positive factor, to the direct product 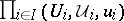 , where
, where 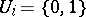 ,
, 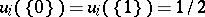 , and the set
, and the set 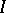 may have arbitrary cardinality (the Maharan–Kolmogorov theorem). If
may have arbitrary cardinality (the Maharan–Kolmogorov theorem). If 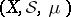 is separable, non-atomic and
is separable, non-atomic and 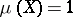 , then it is isomorphic to the space
, then it is isomorphic to the space 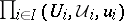 with
with 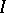 countable, which in turn is isomorphic to the unit interval with the Lebesgue measure.
countable, which in turn is isomorphic to the unit interval with the Lebesgue measure.
Side by side with the theory of measures regarded as functions on subsets of some set, the theory of measures as functions on the elements of a Boolean ring (or on a Boolean algebra) has been developed; these theories are in many respects parallel. Another widespread construction of measures goes back to W. Young and P. Daniell (see [12]). Theories dealing with measures with real or complex values, or with values belonging to some algebraic structure, were developed in addition to the theory of positive measures.
References
| [1] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [2] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [4] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
| [5] | J. Neveu, "Mathematical foundations of the calculus of probabilities" , Holden-Day (1965) (Translated from French) |
| [6] | B.V. Gnedenko, A.N. Kolmogorov, "Limit distributions for sums of independent random variables" , Addison-Wesley (1954) (Translated from Russian) |
| [7] | V.S. Varadarajan, "Measures on topological spaces" Mat. Sb. , 55 : 1 (1961) pp. 35–100 (In Russian) |
| [8] | K.R. Parthasarathy, "Probability measures on metric spaces" , Acad. Press (1967) |
| [9] | P. Billingsley, "Convergence of probability measures" , Wiley (1968) |
| [10] | R. Sikorski, "Boolean algebras" , Springer (1969) |
| [11] | D.A. Vladimirov, "Boolesche Algebren" , Akademie Verlag (1978) (Translated from Russian) |
| [12] | N. Bourbaki, "Elements of mathematics. Integration" , Addison-Wesley (1975) pp. Chapt.6;7;8 (Translated from French) |
| [13] | J. Diestel, J.J. Uhl jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977) |
Comments
Properties 1) and 2) listed under the heading "Properties of measure spaces" are usually called Fatou's lemma, cf. Fatou theorem.
The procedure for extending a measure, as described under the heading "Extension of measures" , is due to C. Carathéodory, and one often speaks of Carathéodory extension, with the accompanying phrases Carathéodory extension theorem and Carathéodory outer (inner) measure (cf. Carathéodory measure).
Recall that a ring (respectively, a 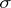 -ring)
-ring) 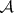 of subsets of a set
of subsets of a set 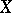 such that
such that 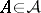 implies
implies 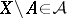 , is called a Boolean algebra or an algebra (respectively, a
, is called a Boolean algebra or an algebra (respectively, a 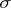 -algebra or a
-algebra or a 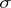 -field, cf. also Algebra of sets). Usually, in a measure space
-field, cf. also Algebra of sets). Usually, in a measure space 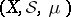 the
the 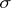 -ring
-ring 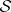 can be proved to be a
can be proved to be a 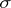 -field (this holds, in particular, if
-field (this holds, in particular, if 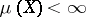 ).
).
The phrase "totally (s-) finite" is seldom used.
Borel has given very nice ideas in order to construct the measure 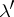 , but Lebesgue was the first to give a satisfactory construction of it, as a byproduct of the construction of
, but Lebesgue was the first to give a satisfactory construction of it, as a byproduct of the construction of 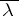 .
.
A product space is also often written as a (kind of) tensor product: 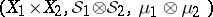 .
.
A family of measurable spaces 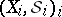 with compatible probability measures on each finite product is called a projective system of measure spaces, and the corresponding probability measure on
with compatible probability measures on each finite product is called a projective system of measure spaces, and the corresponding probability measure on 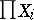 , if it exists, is called the projective limit; it exists if
, if it exists, is called the projective limit; it exists if 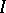 is countable (the Ionescu–Tulcea theorem, cf. [5]).
is countable (the Ionescu–Tulcea theorem, cf. [5]).
Suppose that 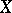 is a topological space and
is a topological space and 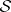 is its Borel
is its Borel 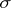 -field; then
-field; then 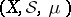 is perfect for every finite measure
is perfect for every finite measure 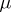 if
if 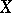 is a Polish space or, more generally, a Luzin space (in which case
is a Polish space or, more generally, a Luzin space (in which case 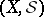 is often called a standard measurable space) or, still more generally, a Suslin space (in which case
is often called a standard measurable space) or, still more generally, a Suslin space (in which case 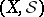 is sometimes called a Blackwell measurable space) (cf. (the editorial comments to) Descriptive set theory).
is sometimes called a Blackwell measurable space) (cf. (the editorial comments to) Descriptive set theory).
The converse part of Prokhorov's theorem is not true when 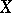 is the space of rational numbers, or, more generally, when
is the space of rational numbers, or, more generally, when 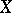 is a Luzin space which is not Polish. See [a1].
is a Luzin space which is not Polish. See [a1].
In the abstract setting, whenever 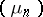 is a sequence of finite measures on
is a sequence of finite measures on 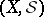 , where
, where 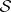 is a
is a 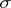 -field, such that
-field, such that
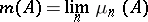 |
exists for any 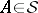 , then
, then 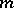 is also a measure (the Vitali–Hahn–Saks theorem, cf. [3] or [5]).
is also a measure (the Vitali–Hahn–Saks theorem, cf. [3] or [5]).
References
| [a1] | D. Preiss, "Metric spaces in which Prokhorov's theorem is not valid" Z. Wahrscheinlichkeitstheor. Verw. Gebiete , 27 (1973) pp. 109–116 |
| [a2] | D. Cohn, "Measure theory" , Birkhäuser (1980) |
| [a3] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , I , Springer (1979) |
| [a4] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
Measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measure&oldid=18607