Mahler measure
Given a polynomial 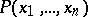 with complex coefficients, the logarithmic Mahler measure
with complex coefficients, the logarithmic Mahler measure 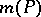 is defined to be the average over the unit
is defined to be the average over the unit  -torus of
-torus of 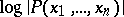 , i.e.
, i.e.
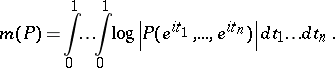 |
The Mahler measure is defined by 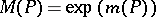 , so that
, so that 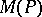 is the geometric mean of
is the geometric mean of  over the
over the  -torus. If
-torus. If 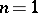 and
and 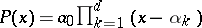 , Jensen's formula gives the explicit formula
, Jensen's formula gives the explicit formula
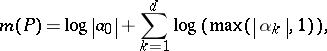 |
so that  .
.
The Mahler measure is useful in the study of polynomial inequalities because of the multiplicative property 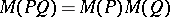 . The important basic inequality
. The important basic inequality
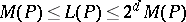 |
[a9] relates  to
to 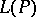 , the sum of the absolute values of the coefficients of
, the sum of the absolute values of the coefficients of 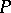 , where
, where 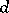 denotes the total degree of
denotes the total degree of 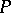 , i.e. the sum of the degrees in each variable separately. A recent inequality for polynomials of one variable is that
, i.e. the sum of the degrees in each variable separately. A recent inequality for polynomials of one variable is that 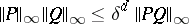 , where
, where 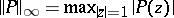 ,
, 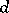 is the sum of the degrees of
is the sum of the degrees of 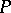 and
and 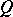 , and
, and 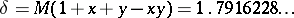 is the best possible constant [a2].
is the best possible constant [a2].
Specializing to polynomials with integer coefficients, in case  ,
, 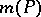 is the logarithm of an algebraic integer (cf. Algebraic number). If
is the logarithm of an algebraic integer (cf. Algebraic number). If 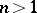 , there are few explicit formulas known, but those that do exist suggest that
, there are few explicit formulas known, but those that do exist suggest that 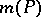 has intimate connections with
has intimate connections with 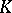 -theory. For example,
-theory. For example, 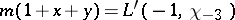 , where
, where 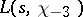 is the Dirichlet
is the Dirichlet 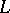 -function for the odd primitive character of conductor
-function for the odd primitive character of conductor  , i.e.
, i.e. 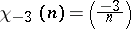 , and it has been conjectured that
, and it has been conjectured that 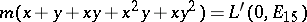 , where
, where 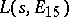 is the
is the 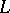 -function of an elliptic curve of conductor
-function of an elliptic curve of conductor 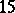 . This formula has not been proved but has been verified to over
. This formula has not been proved but has been verified to over 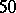 decimal places [a3], [a4].
decimal places [a3], [a4].
The Mahler measure 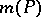 occurs naturally as the growth rate in many problems, for example as the entropy of certain
occurs naturally as the growth rate in many problems, for example as the entropy of certain 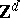 -actions [a10]. The set of
-actions [a10]. The set of  for which
for which 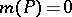 is known: in case
is known: in case 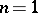 , a theorem of Kronecker shows that these are products of cyclotomic polynomials and monomials. In case
, a theorem of Kronecker shows that these are products of cyclotomic polynomials and monomials. In case 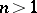 , these are the generalized cyclotomic polynomials [a1]. An important open question, known as Lehmer's problem, is whether there is a constant
, these are the generalized cyclotomic polynomials [a1]. An important open question, known as Lehmer's problem, is whether there is a constant 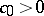 such that if
such that if 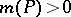 , then
, then 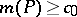 . This is known to be the case if
. This is known to be the case if 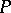 is a non-reciprocal polynomial, where a polynomial is reciprocal if
is a non-reciprocal polynomial, where a polynomial is reciprocal if 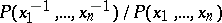 is a monomial. In this case,
is a monomial. In this case, 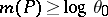 , where
, where 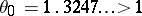 is the smallest Pisot number, the real root of
is the smallest Pisot number, the real root of 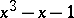 [a6], [a1]. A possible value for
[a6], [a1]. A possible value for 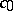 is
is 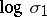 , where
, where 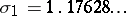 is the smallest known Salem number, a number of degree
is the smallest known Salem number, a number of degree 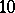 known as Lehmer's number.
known as Lehmer's number.
For 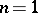 , the best result in this direction is that
, the best result in this direction is that 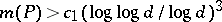 , where
, where 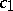 is an explicit absolute constant and
is an explicit absolute constant and 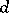 is the degree of
is the degree of 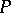 [a5]. A result that applies to polynomials in any number of variables is an explicit constant
[a5]. A result that applies to polynomials in any number of variables is an explicit constant 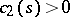 depending on the number
depending on the number  of non-zero coefficients of
of non-zero coefficients of 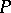 such that
such that 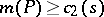 [a7], [a1].
[a7], [a1].
A recent development is the elliptic Mahler measure [a8], in which the torus 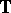 is replaced by an elliptic curve. It seems likely that this will have an interpretation as the entropy of a dynamical system but this remains as of yet (1998) a future development.
is replaced by an elliptic curve. It seems likely that this will have an interpretation as the entropy of a dynamical system but this remains as of yet (1998) a future development.
References
| [a1] | D.W. Boyd, "Kronecker's theorem and Lehmer's problem for polynomials in several variables" J. Number Th. , 13 (1981) pp. 116–121 |
| [a2] | D.W. Boyd, "Two sharp inequalities for the norm of a factor of a polynomial" Mathematika , 39 (1992) pp. 341–349 |
| [a3] | D.W. Boyd, "Mahler's measure and special values of 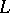 -functions" Experim. Math. , 37 (1998) pp. 37–82 -functions" Experim. Math. , 37 (1998) pp. 37–82 |
| [a4] | C. Deninger, "Deligne periods of mixed motives, 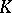 -theory and the entropy of certain -theory and the entropy of certain 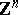 -actions" J. Amer. Math. Soc. , 10 (1997) pp. 259–281 -actions" J. Amer. Math. Soc. , 10 (1997) pp. 259–281 |
| [a5] | E. Dobrowolski, "On a question of Lehmer and the number of irreducible factors of a polynomial" Acta Arith. , 34 (1979) pp. 391–401 |
| [a6] | C.J. Smyth, "On the product of the conjugates outside the unit circle of an algebraic integer" Bull. London Math. Soc. , 3 (1971) pp. 169–175 |
| [a7] | E. Dobrowolski, "Mahler's measure of a polynomial in function of the number of its coefficients" Canad. Math. Bull. , 34 (1991) pp. 186–195 |
| [a8] | G. Everest, Ni Fhlathúin Brid, "The elliptic Mahler measure" Math. Proc. Cambridge Philos. Soc. , 120 : 1 (1996) pp. 13–25 |
| [a9] | K. Mahler, "On some inequalities for polynomials in several variables" J. London Math. Soc. , 37 : 2 (1962) pp. 341–344 |
| [a10] | K. Schmidt, "Dynamical systems of algebraic origin" , Birkhäuser (1995) |
Mahler measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mahler_measure&oldid=18597