Restricted quantifier
A quantifier applied to predicates not with respect to the whole range of a given object variable, but with respect to a part of it defined by a predicate 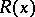 . When used in this restricted sense, the universal quantifier
. When used in this restricted sense, the universal quantifier 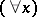 and the existential quantifier
and the existential quantifier 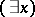 are usually denoted by
are usually denoted by 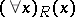 and
and 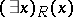 (or
(or 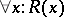 and
and 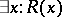 , respectively). If
, respectively). If 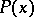 is a predicate, then
is a predicate, then  means
means
 |
that is, the predicate 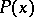 is true for all values of the variable
is true for all values of the variable  satisfying the predicate
satisfying the predicate 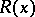 . The proposition
. The proposition 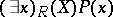 means
means
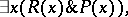 |
that is, the intersection of the truth domains of the predicates 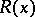 and
and 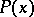 is non-empty.
is non-empty.
Restricted quantifiers of the form 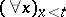 and
and 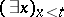 (more commonly called bounded quantifiers) play an important role in formal arithmetic (cf. Arithmetic, formal), where
(more commonly called bounded quantifiers) play an important role in formal arithmetic (cf. Arithmetic, formal), where 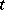 is a term not containing
is a term not containing  . When these quantifiers are applied to a decidable predicate, the result is a decidable predicate.
. When these quantifiers are applied to a decidable predicate, the result is a decidable predicate.
Restricted quantifier. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Restricted_quantifier&oldid=18590