Brun-Titchmarsh theorem
For coprime integers  and
and  , let
, let  denote the number of primes not exceeding
denote the number of primes not exceeding  that are congruent to
that are congruent to  modulo
modulo  . Using analytic methods of the theory of
. Using analytic methods of the theory of  -functions [a8], one can show that the asymptotic formula
-functions [a8], one can show that the asymptotic formula
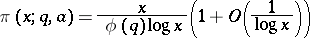 |
holds uniformly for 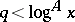 , where
, where  is an arbitrary positive constant. It is desirable to extend the validity range for
is an arbitrary positive constant. It is desirable to extend the validity range for  of this formula, in view of its applications to classical problems. The generalized Riemann hypothesis (cf. Riemann hypotheses) is not capable of providing any information for
of this formula, in view of its applications to classical problems. The generalized Riemann hypothesis (cf. Riemann hypotheses) is not capable of providing any information for 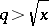 .
.
In contrast, a simple application of a sieve method [a8] leads to an upper bound which gives the correct order of magnitude of  for all
for all 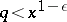 , where
, where  is an arbitrary positive constant. Because of its uniformity in
is an arbitrary positive constant. Because of its uniformity in 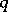 , an inequality of this type turns out to be very useful [a3], [a5], [a8]; it is known as the Brun–Titchmarsh theorem. By a sophisticated argument, [a6], one finds that
, an inequality of this type turns out to be very useful [a3], [a5], [a8]; it is known as the Brun–Titchmarsh theorem. By a sophisticated argument, [a6], one finds that
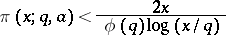 |
for all 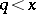 . The constant
. The constant  possesses a significant meaning in the context of sieve methods [a2], [a7]. By adapting the Brun–Titchmarsh theorem [a1], [a4], if necessary, it is possible to sharpen the above bound in various ranges for
possesses a significant meaning in the context of sieve methods [a2], [a7]. By adapting the Brun–Titchmarsh theorem [a1], [a4], if necessary, it is possible to sharpen the above bound in various ranges for 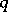 .
.
References
| [a1] | E. Fouvry, "Théorème de Brun–Titchmarsh: application au théorème de Fermat" Invent. Math. , 79 (1985) pp. 383–407 |
| [a2] | H. Halberstam, H.E. Richert, "Sieve methods" , Acad. Press (1974) |
| [a3] | C. Hooley, "Applications of sieve methods to the theory of numbers" , Cambridge Univ. Press (1976) |
| [a4] | H. Iwaniec, "On the Brun–Titchmarsh theorem" J. Math. Soc. Japan , 34 (1982) pp. 95–123 |
| [a5] | Yu.V. Linnik, "Dispersion method in binary additive problems" , Nauka (1961) (In Russian) |
| [a6] | H.L. Montgomery, R.C. Vaughan, "The large sieve" Mathematika , 20 (1973) pp. 119–134 |
| [a7] | Y. Motohashi, "Sieve methods and prime number theory" , Tata Institute and Springer (1983) |
| [a8] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
Brun-Titchmarsh theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Brun-Titchmarsh_theorem&oldid=18569