Jacobi variety

Jacobian, Jacobian variety, of an algebraic curve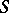

The principally polarized Abelian variety (cf. also Polarized algebraic variety) 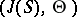formed from this curve. Sometimes a Jacobi variety is simply considered to be a commutative algebraic group. If 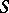is a smooth projective curve of genus 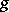over the field 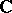, or, in classical terminology, a compact Riemann surface of genus 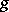, then the integration of holomorphic 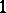-forms over the 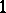-cycles on 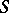defines the imbedding

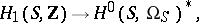the image of which is a lattice of maximal rank (here 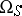denotes the bundle of holomorphic 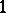-forms on 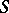). The Jacobi variety of the curve 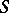is the quotient variety

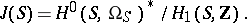For the polarization on it one can take the cohomology class 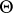from

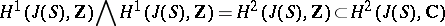that corresponds to the intersection form on 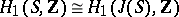. This polarization is principal, that is, 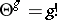. For a more explicit definition of a Jacobi variety it is usual to take a basis 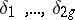in 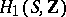and a basis of forms 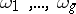in 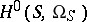. These define a 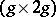-matrix — the matrix of periods of the Riemann surface:

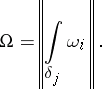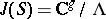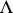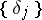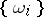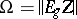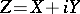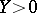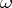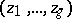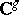Then , where is the lattice with basis consisting of the columns of . The bases and can be chosen so that ; here the matrix is symmetric and (see Abelian differential). The polarization class is represented by the form that, when written in standard coordinates in , is

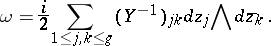Often, instead of the cohomology class 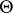the effective divisor dual to it is considered; it is denoted by the same letter and is defined uniquely up to a translation. Geometrically, the divisor 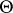can be described in the following way. Consider the Abelian mapping 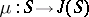defined by

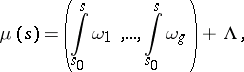where 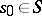is fixed. Let 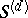be the 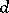-th symmetric power of 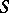, that is, the quotient variety of the variety 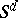with respect to the symmetric group (the points of 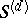correspond to effective divisors of degree 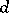on 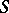). The formula defines an extension of the Abelian mapping to 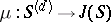. Then .

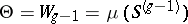The equivalence relation in 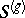defined by 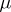coincides with the rational equivalence of divisors (Abel's theorem). In addition, 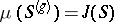(Jacobi's inversion theorem). C.G.J. Jacobi

studied the inversion problem in the case 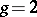(see also Jacobi inversion problem). The above-mentioned theorems determine an isomorphism 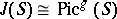, where 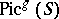is the component of the Picard group 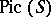corresponding to divisors of degree 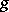. Multiplication by the divisor class 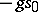leads to a canonical isomorphism 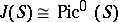of Abelian varieties.

In the case of a complete smooth curve over an arbitrary field, the Jacobi variety 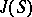is defined as the Picard variety 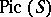. The Abelian mapping 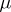associates with a point 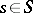the class of the divisor 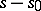, and the polarization is defined by the divisor .

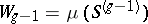The significance of Jacobi varieties in the theory of algebraic curves is clear from the Torelli theorem (cf. Torelli theorems): A non-singular complete curve is uniquely defined by its Jacobian (with due regard for polarization) (see [5]). The passage from a curve to its Jacobian enables one to linearize a number of non-linear problems in the theory of curves. For example, the problem of describing special divisors on 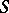(that is, effective divisors 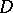for which 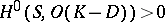) is essentially translated to the language of singularities of special subvarieties 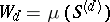of 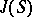. This translation is based on the Riemann–Kempf theorem about singularities (see , [5]). One of the corollaries of this theorem is that the codimension of the variety of singular points of the divisor of the polarization, 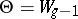, does not exceed 4. This property of Jacobi varieties is characteristic if one considers only principally polarized Abelian varieties belonging to a neighbourhood of the Jacobian of a general curve. 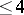More precisely, if the variety of singular points of the divisor of the polarization of a principally polarized Abelian variety has codimension , and if 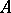does not belong to several distinguished components of the moduli variety, then 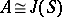for a smooth curve 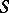(see [2]).

Another approach to distinguishing Jacobians among Abelian varieties is to define equations in 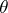-functions and their derivatives at special points. The problem of finding these equations is called Schottky's problem.

In the case of a singular curve 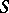the Jacobi variety 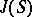is regarded as the subgroup of 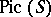defined by divisors of degree 0 with respect to each irreducible component of 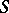(it coincides with the connected component of the identity in 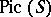). If the curve 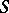is defined by a module 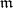on a smooth model 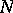, then 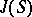is usually called the generalized Jacobian of the curve 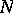(relative to 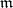), and is denoted by 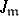(see [6]).

References

[1a]	C.G.J. Jacobi, "Considerationes generales de transcendentibus abelianis" J. Reine Angew. Math. , 9 (1832) pp. 349–403
[1b]	C.G.J. Jacobi, "De functionibus duarum variabilium quadrupliciter periodicis, quibus theoria transcendentium abelianarum innititur" J. Reine Angew. Math. , 13 (1835) pp. 55–78
[2]	A. Andreotti, A. Mayer, "On period relations for abelian integrals on algebraic curves" Ann. Scu. Norm. Sup. Pisa , 21 (1967) pp. 189–238
[3]	P.A. Griffiths, "An introduction to the theory of special divisors on algebraic curves" , Amer. Math. Soc. (1980)
[4]	D. Mumford, "Curves and their Jacobians" , Univ. Michigan Press (1978)
[5]	P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978)
[6]	J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959)

Comments

The Schottky problem has been solved, cf. Schottky problem.

Here, a module on a smooth curve 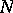is simply an effective divisor, i.e. a finite set 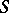of points of 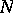with a positive integer 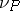assigned to each point 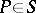. Given a module 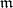and a rational functi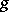on on 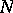, one writes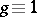 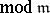if 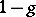has a zero of order 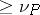in 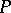for all 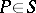. Consider divisors 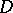whose support does not intersect 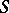. For these divisors one defines an equivalence relation: 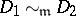if there is a rational function 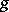such that 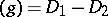and 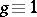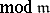. This is the equivalence relation that serves to define the generalized Jacobian 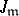, cf. [6], Chapt. V for details. In general, the generalized Jacobian is not complete; it is an extension of 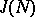by a connected linear algebraic group. Every Abelian extension of the function field of 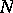can be obtained by an isogeny of a generalized Jacobian. This is a main reason for studying them, [6].

In the case of an arbitrary field the construction of the Jacobi variety 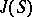of a complete smooth curve 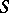was achieved by A. Weil, first as an abstract algebraic variety (see [a1] and [a2]), and later as a projective variety by W.L. Chow (see [a3]).

For the theory of the singularities of the 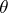-divisor and for the Torelli theorem see also [a4].

References

[a1]	A. Weil, "Courbes algébriques et variétés abéliennes. Variétés abéliennes et courbes algébriques" , Hermann (1971)
[a2]	S. Lang, "Abelian varieties" , Springer (1981)
[a3]	W.L. Chow, "The Jacobian variety of an algebraic curve" Amer. J. Math. , 76 (1954) pp. 453–476
[a4]	E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1985)