Pearson product-moment correlation coefficient
While the modern theory of correlation and regression has its roots in the work of F. Galton, the version of the product-moment correlation coefficient in current use (2000) is due to K. Pearson [a2]. Pearson's product-moment correlation coefficient  is a measure of the strength of a linear relationship between two random variables
is a measure of the strength of a linear relationship between two random variables  and
and  (cf. also Random variable) with means
(cf. also Random variable) with means  ,
,  and finite variances
and finite variances  ,
,  :
:
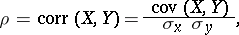 |
where  is the covariance of
is the covariance of 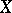 and
and  ,
,
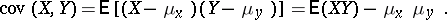 |
It readily follows that  , and that
, and that  is equal to
is equal to  or
or 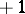 if and only if each of
if and only if each of 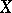 and
and  is almost surely a linear function of the other, i.e.,
is almost surely a linear function of the other, i.e.,  (
(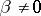 ) with probability
) with probability  (furthermore,
(furthermore,  and
and  have the same sign). If
have the same sign). If  ,
,  and
and  are said to be uncorrelated. Independent random variables are always uncorrelated, however uncorrelated random variables need not be independent (cf. also Independence).
are said to be uncorrelated. Independent random variables are always uncorrelated, however uncorrelated random variables need not be independent (cf. also Independence).
The term "product-moment" refers to the observation that  , where
, where  denotes the
denotes the  th product moment of
th product moment of  and
and  about their means.
about their means.
The coefficient 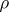 also plays a role in linear regression (cf. also Regression analysis). If the regression of
also plays a role in linear regression (cf. also Regression analysis). If the regression of 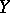 on
on  is linear, then
is linear, then  , and if the regression of
, and if the regression of  on
on  is linear, then
is linear, then 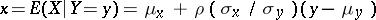 . Note that the product of the two slopes is
. Note that the product of the two slopes is 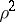 .
.
When  and
and  have a bivariate normal distribution (cf. also Normal distribution),
have a bivariate normal distribution (cf. also Normal distribution),  is a parameter of the joint density function
is a parameter of the joint density function
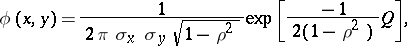 |
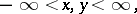 |
with
 |
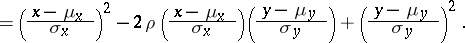 |
Unlike the general situation, uncorrelated random variables with a bivariate normal distribution are independent.
For a random sample  from a bivariate population,
from a bivariate population, 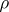 is estimated by the sample correlation coefficient (cf. also Correlation coefficient)
is estimated by the sample correlation coefficient (cf. also Correlation coefficient)  , given by
, given by
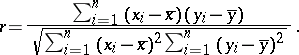 |
If  and
and  denote, respectively, the vectors
denote, respectively, the vectors  and
and  , and
, and 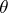 denotes the angle between
denotes the angle between  and
and 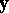 , then
, then
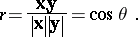 |
Further interpretations of  can be found in [a3]. For details on the use of
can be found in [a3]. For details on the use of  in hypothesis testing, and for large-sample theory, see [a1].
in hypothesis testing, and for large-sample theory, see [a1].
References
| [a1] | O.J. Dunn, V.A. Clark, "Applied statistics: analysis of variance and regression" , Wiley (1974) |
| [a2] | K. Pearson, "Mathematical contributions to the theory of evolution. III. Regression, heredity and panmixia" Philos. Trans. Royal Soc. London Ser. A , 187 (1896) pp. 253–318 |
| [a3] | J.L. Rodgers, W.A. Nicewander, "Thirteen ways to look at the correlation coefficient" The Amer. Statistician , 42 (1988) pp. 59–65 |
Pearson product-moment correlation coefficient. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pearson_product-moment_correlation_coefficient&oldid=18562