Arithmetic group

A subgroup of a linear algebraic group defined over the field of rational numbers, that satisfies the following condition: There exists a faithful rational representation defined over (cf. Representation theory) such that is commensurable with , where is the ring of integers (two subgroups and 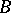of a group are called commensurable if is of finite index in and in ). This condition is then also satisfied for any other faithful representation defined over 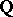. More generally, an arithmetic group is a subgroup of an algebraic group , defined over a global field , that is commensurable with the group of -points of 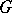, where is the ring of integers of 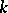. An arithmetic group 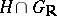is a discrete subgroup of .

If 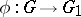is a 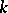-epimorphism of algebraic groups, then the image 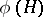of any arithmetic group is an arithmetic group in 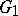[1]. The name arithmetic group is sometimes also given to an abstract group that is isomorphic to an arithmetic subgroup of some algebraic group. Thus, if is an algebraic number field, the group , where 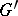is obtained from 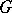by restricting the field of definition from 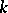to , is called an arithmetic group. In the theory of Lie groups the name arithmetic subgroups is also given to images of arithmetic subgroups of the group of real points of under the factorization of 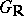by compact normal subgroups.

References

[1]	A. Borel, "Ensembles fundamentaux pour les groups arithmétiques et formes automorphes" , Fac. Sci. Paris (1967)
[2]	A. Borel, Harish-Chandra, "Arithmetic subgroups of algebraic groups" Ann. of Math. , 75 (1962) pp. 485–535
[3]	, Arithmetic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966)

Comments

Useful additional references are [a1]–[a3]. [a2] is an elementary introduction to the theory of arithmetic groups.

Conjectures of A. Selberg and I.I. Pyatetskii-Shapiro roughly state that for most semi-simple Lie groups discrete subgroups of finite co-volume are necessarily arithmetic. G.A. Margulis settled this question completely and, in particular, proved the conjectures in question. See Discrete subgroup for more detail.

References

[a1]	A. Borel, "Arithmetic properties of linear algebraic groups" , Proc. Internat. Congress mathematicians (Stockholm, 1962) , Inst. Mittag-Leffler (1963) pp. 10–22
[a2]	A. Borel, "Introduction aux groupes arithmétiques" , Hermann (1969)
[a3]	J.E. Humphreys, "Arithmetic groups" , Springer (1980)