Parameter-dependent integral
An integral of the type
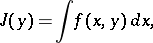 |
in which the point  ranges over the space
ranges over the space  (if the point ranges only over a certain domain
(if the point ranges only over a certain domain 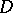 in
in 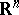 , the function
, the function 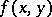 may be assumed to vanish for
may be assumed to vanish for 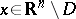 ), while the point
), while the point 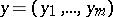 , representing a set of parameters
, representing a set of parameters 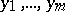 , varies within some domain
, varies within some domain 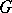 of the space
of the space 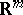 .
.
The main concern of the theory of such integrals is to determine conditions for the continuity and differentiability of 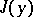 with respect to the parameters
with respect to the parameters 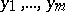 . If
. If 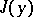 is interpreted as a Lebesgue integral, one obtains less restrictive conditions for its continuity and differentiability. The following propositions are valid.
is interpreted as a Lebesgue integral, one obtains less restrictive conditions for its continuity and differentiability. The following propositions are valid.
1) If 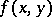 is continuous in
is continuous in 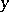 in the domain
in the domain 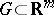 for almost-all
for almost-all  and if there exists an integrable function
and if there exists an integrable function 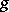 on
on 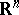 such that
such that 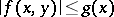 for every
for every 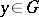 and almost-all
and almost-all  , then
, then 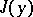 is continuous in
is continuous in 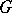 .
.
2) Let 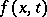 be a function defined for
be a function defined for  ,
, 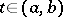 . Assume that the derivative
. Assume that the derivative 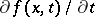 exists for almost-all
exists for almost-all  and every
and every 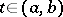 and that is a continuous function of
and that is a continuous function of 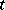 on
on 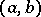 for almost-all
for almost-all  . Assume, moreover, that there exists an integrable function
. Assume, moreover, that there exists an integrable function 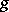 on
on 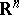 such that
such that 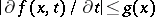 for every
for every 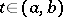 and almost-all
and almost-all  . Finally, assume that for some
. Finally, assume that for some 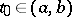 the integral
the integral
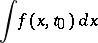 |
exists. Then the function
 |
is differentiable with respect to  on
on 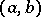 , and its derivative
, and its derivative 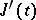 may be evaluated by differentiating under the integral sign:
may be evaluated by differentiating under the integral sign:
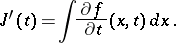 |
These two propositions imply a series of simpler propositions about the continuity and differentiability of integrals with parameters, relating to the interpretation of the integral as a Riemann integral and to more specific cases (see [2]–[4]).
Parameter-dependent improper integrals.
For the simplest improper integral of the first kind,
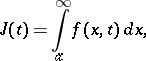 | (*) |
one introduces the notion of uniform convergence with respect to the parameter 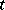 in a closed interval
in a closed interval 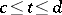 . This integral is said to be uniformly convergent in
. This integral is said to be uniformly convergent in 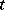 on
on 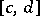 if, for each
if, for each 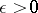 , there exists an
, there exists an 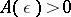 such that
such that
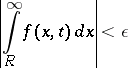 |
for all  .
.
The following propositions are valid.
a) If 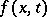 is continuous in a half-strip
is continuous in a half-strip 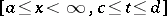 and if the integral (*) is uniformly convergent in
and if the integral (*) is uniformly convergent in 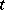 on
on 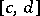 , then
, then 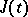 is continuous in
is continuous in  .
.
b) If 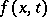 and the derivative
and the derivative  are continuous in a half-strip
are continuous in a half-strip 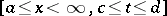 , if the integral (*) is convergent for some
, if the integral (*) is convergent for some 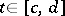 and if the integral
and if the integral
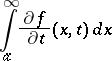 |
is uniformly convergent in 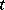 on
on 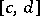 , then the function
, then the function 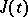 is differentiable on
is differentiable on 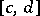 and its derivative may be evaluated by the formula
and its derivative may be evaluated by the formula
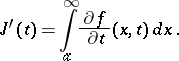 |
Analogous propositions hold for improper integrals of the second kind.
References
| [1] | V.S. Vladimirov, "Equations of mathematical physics" , MIR (1984) (Translated from Russian) |
| [2] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 2 , MIR (1982) (Translated from Russian) |
| [3] | L.D. Kudryavtsev, "Mathematical analysis" , 2 , Moscow (1970) (In Russian) |
| [4] | S.M. Nikol'skii, "A course of mathematical analysis" , 2 , MIR (1977) (Translated from Russian) |
| [5] | A.N. [A.N. Tikhonov] Tichonoff, A.A. Samarskii, "Differentialgleichungen der mathematischen Physik" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
Comments
The propositions stated are simple consequences of Lebesgue's dominated convergence principle (see Lebesgue theorem 2)).
Parameter-dependent integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Parameter-dependent_integral&oldid=18531