Saddle point in game theory
A point  of a function
of a function  defined on the Cartesian product
defined on the Cartesian product  of two sets
of two sets  and
and  such that
such that
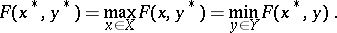 | (*) |
For a function  the presence of a saddle point is equivalent to the existence of optimal strategies (cf. Strategy (in game theory)) for the players in the two-person zero-sum game
the presence of a saddle point is equivalent to the existence of optimal strategies (cf. Strategy (in game theory)) for the players in the two-person zero-sum game  .
.
Comments
A point  satisfying the condition (*) is called a saddle point of
satisfying the condition (*) is called a saddle point of  in general. If
in general. If  is a differentiable function on
is a differentiable function on  and
and  ,
,  , while the Hessian matrix
, while the Hessian matrix 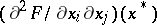 is non-singular and neither positive definite nor negative definite, then locally near
is non-singular and neither positive definite nor negative definite, then locally near 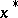 ,
,  is a saddle point. The corresponding splitting of
is a saddle point. The corresponding splitting of  near
near  is determined by the negative and positive eigenspaces of the Hessian at
is determined by the negative and positive eigenspaces of the Hessian at 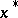 .
.
Indeed, by the Morse lemma there are coordinates  near
near 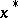 such that
such that 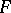 has the form
has the form
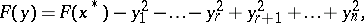 |
where  is the index of the quadratic form determined by the symmetric matrix
is the index of the quadratic form determined by the symmetric matrix 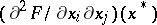 . (The index of a quadratic form is the dimension of the largest subspace on which it is negative definite; this is also called the negative index of inertia (cf. also Quadratic form and Morse index).)
. (The index of a quadratic form is the dimension of the largest subspace on which it is negative definite; this is also called the negative index of inertia (cf. also Quadratic form and Morse index).)
Let 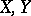 be the spaces of strategies of two players in a zero-sum game and let
be the spaces of strategies of two players in a zero-sum game and let 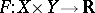 be (the first component of) the pay-off function (cf. Games, theory of). Then a saddle point is also called an equilibrium point. This notion generalizes to
be (the first component of) the pay-off function (cf. Games, theory of). Then a saddle point is also called an equilibrium point. This notion generalizes to  -player non-cooperative games, cf. [a2], Chapt. 2; Games, theory of; Nash theorem (in game theory); Non-cooperative game.
-player non-cooperative games, cf. [a2], Chapt. 2; Games, theory of; Nash theorem (in game theory); Non-cooperative game.
References
| [a1] | M.W. Hirsch, "Differential topology" , Springer (1976) pp. Chapt. 6 |
| [a2] | J. Szép, F. Forgó, "Introduction to the theory of games" , Reidel (1985) pp. 171; 199 |
Saddle point in game theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Saddle_point_in_game_theory&oldid=18503