Asymptotically-unbiased test
From Encyclopedia of Mathematics
A concept indicating that the test is unbiased in the limit. For example, in the case of 
independent samples from a one-dimensional distribution depending on a parameter 
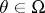, let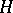 
be the null hypothesis: 
, and let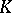 
be the alternative:
 |
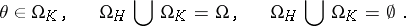The critical set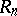 
in the 
-dimensional Euclidean space, 
is an asymptotically-unbiased test of the hypothesis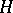 
with level 
if
 |
 |
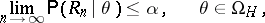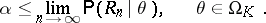The function
 |
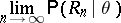is called the asymptotic power function of the test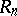 
.
How to Cite This Entry:
Asymptotically-unbiased test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotically-unbiased_test&oldid=18499
Asymptotically-unbiased test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotically-unbiased_test&oldid=18499
This article was adapted from an original article by O.V. Shalaevskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article