Runge rule
One of the methods for estimating errors in numerical integration formulas (cf. Integration, numerical). Let 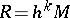 be the residual term in a numerical integration formula, where
be the residual term in a numerical integration formula, where 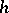 is the length of the integration interval or of some part of it,
is the length of the integration interval or of some part of it, 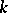 is a fixed number and
is a fixed number and 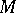 is the product of a constant with the
is the product of a constant with the 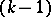 -st derivative of the integrand at some point of the integration interval. If
-st derivative of the integrand at some point of the integration interval. If 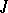 is the exact value of an integral and
is the exact value of an integral and 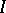 is its approximate value, then
is its approximate value, then 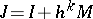 .
.
According to Runge's rule, the same integral is calculated by the same numerical integration formula, but instead of 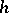 one takes the value
one takes the value 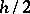 . Also, to obtain the value of the integral over the entire interval the integration formula is applied twice. If the derivative in
. Also, to obtain the value of the integral over the entire interval the integration formula is applied twice. If the derivative in 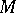 does not change too strongly on the considered interval, then
does not change too strongly on the considered interval, then
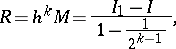 |
where 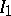 is the value of the integral calculated with respect to
is the value of the integral calculated with respect to 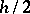 .
.
Runge's rule is also used when numerically solving differential equations. The rule was proposed by C. Runge (beginning of the 20th century).
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [2] | G. Hall (ed.) J.M. Watt (ed.) , Modern numerical methods for ordinary differential equations , Clarendon Press (1976) |
Runge rule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Runge_rule&oldid=18486