Free product of groups
 ,
, 
A group  generated by the groups
generated by the groups  such that any homomorphisms
such that any homomorphisms  of the
of the  into an arbitrary group
into an arbitrary group  can be extended to a homomorphism
can be extended to a homomorphism  . The symbol * is used to denote a free product, for example,
. The symbol * is used to denote a free product, for example,
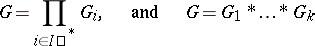 |
in the case of a finite set 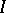 . Each element of a free product
. Each element of a free product 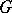 that is not the identity can be expressed uniquely as an irreducible word
that is not the identity can be expressed uniquely as an irreducible word 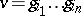 , where
, where 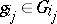 ,
, 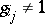 and
and 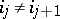 for any
for any 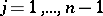 . The construction of a free product is important in the study of groups defined by a set of generating elements and defining relations. In these terms it can be defined as follows. Suppose that each group
. The construction of a free product is important in the study of groups defined by a set of generating elements and defining relations. In these terms it can be defined as follows. Suppose that each group 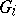 is defined by sets
is defined by sets 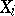 of generators and
of generators and 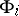 of defining relations, where
of defining relations, where 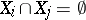 if
if 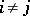 . Then the group
. Then the group  defined by the set
defined by the set  of generators and the set
of generators and the set 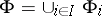 of defining relations is the free product of the groups
of defining relations is the free product of the groups 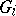 ,
, 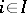 .
.
Every subgroup of a free product 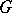 can be decomposed into a free product of subgroups, of which some are infinite cyclic and each of the others is conjugate with some subgroup of a group
can be decomposed into a free product of subgroups, of which some are infinite cyclic and each of the others is conjugate with some subgroup of a group 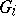 in the free decomposition of
in the free decomposition of 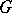 (Kurosh' theorem).
(Kurosh' theorem).
References
| [1] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) |
| [2] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) |
Comments
The notion of a free product of groups is a special case of that of a free product with amalgamated subgroup (see Amalgam of groups).
Free product of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Free_product_of_groups&oldid=18482