Material derivative method
In the study of motion in continuum mechanics one deals with the time rates of changes of quantities that vary from one particle to the other. Such quantities include displacement, velocity and acceleration. These quantities may be expressed as functions described in the material form or the spatial form, and the meaning of the time rate of their change depends on the nature of the description.
Material time derivative.
Consider a real-valued function 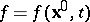 that represents a scalar or a component of a vector or tensor. The point
that represents a scalar or a component of a vector or tensor. The point 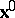 determines a continuum particle uniquely, namely the one located at
determines a continuum particle uniquely, namely the one located at 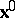 . With this notation, the function
. With this notation, the function  can be interpreted as the value of
can be interpreted as the value of 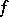 experienced at time
experienced at time 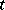 by the particle
by the particle 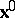 . The time derivative of
. The time derivative of 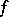 with respect to time
with respect to time 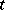 , with
, with 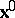 held fixed, is interpreted as the time rate of change of
held fixed, is interpreted as the time rate of change of 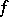 at the particle
at the particle 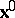 . This derivative is usually called the particle or material time derivative of
. This derivative is usually called the particle or material time derivative of 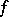 , denoted by
, denoted by 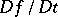 and defined by
and defined by
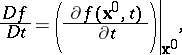 | (a1) |
where the subscript 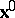 accompanying the vertical line indicates that
accompanying the vertical line indicates that 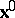 is kept constant in the differentiation of
is kept constant in the differentiation of 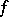 . Note that, like
. Note that, like  ,
,  is a function of
is a function of 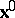 and
and  by definition. In other words,
by definition. In other words, 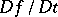 defined above is a function in the material form.
defined above is a function in the material form.
Local time derivative.
In order to define the local time derivative, one considers a real-valued function 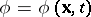 that represents a scalar or a component of a vector or tensor. Since
that represents a scalar or a component of a vector or tensor. Since  is point in the current configuration of a continuum,
is point in the current configuration of a continuum, 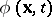 can be interpreted as the value of
can be interpreted as the value of 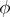 at the point
at the point  at time
at time 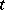 . The partial derivative of
. The partial derivative of 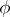 with respect to time
with respect to time 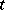 , with
, with  held fixed, is interpreted as the time rate of change of
held fixed, is interpreted as the time rate of change of 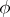 at the particle located at
at the particle located at  . This derivative is called the local time derivative of
. This derivative is called the local time derivative of 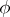 , denoted by the usual partial derivative symbol
, denoted by the usual partial derivative symbol 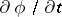 and defined by
and defined by
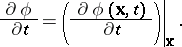 | (a2) |
It is noted that, like 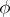 ,
, 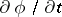 is a function of
is a function of  and
and  , and is a function in the spatial form.
, and is a function in the spatial form.
The distinction between the material time derivative and the local time derivative should be emphasized. While both are partial derivatives with respect to 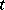 , the former is defined for a function of
, the former is defined for a function of 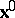 and
and 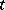 whereas the latter is defined for a function of
whereas the latter is defined for a function of  and
and 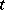 . Physically, the local time derivative of a function represents the rate at which the function changes with time as seen by an observer currently (momentarily) stationed at a point, whereas the material time derivative represents the rate at which the function changes with time as seen by an observer stationed at a particle and moving with it. The material time derivative is therefore also called the mobile time derivative or the derivative following a particle. For brevity, the material time derivative will be referred to as the material derivative or material rate, and the local time derivative as the local derivative or local rate.
. Physically, the local time derivative of a function represents the rate at which the function changes with time as seen by an observer currently (momentarily) stationed at a point, whereas the material time derivative represents the rate at which the function changes with time as seen by an observer stationed at a particle and moving with it. The material time derivative is therefore also called the mobile time derivative or the derivative following a particle. For brevity, the material time derivative will be referred to as the material derivative or material rate, and the local time derivative as the local derivative or local rate.
Velocity and acceleration.
Since  is a function of
is a function of 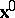 and
and 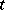 in the material description of motion, the material derivative
in the material description of motion, the material derivative 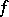 is denoted by
is denoted by  and is defined by
and is defined by
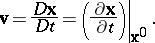 | (a3) |
Evidently,  represents the time rate of change of position of the particle
represents the time rate of change of position of the particle 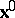 at time
at time 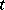 . This is called the velocity of the particle
. This is called the velocity of the particle  at time
at time 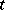 . If
. If 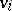 are the components of
are the components of  , then the velocity components of the particle
, then the velocity components of the particle 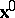 at time
at time 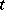 take the form
take the form
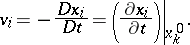 | (a4) |
The displacement vector 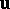 of the particle
of the particle 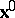 is defined as
is defined as 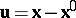 . Thus,
. Thus, 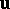 may be regarded as a function of
may be regarded as a function of 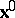 and
and 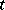 , or of
, or of  and
and 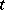 . Treating
. Treating  as a function of
as a function of  and
and 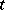 , it follows from the above that
, it follows from the above that
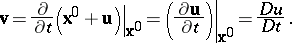 | (a5) |
Thus, the velocity of a particle at time 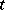 is precisely the rate of change of displacement of that particle at time
is precisely the rate of change of displacement of that particle at time 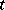 . The above definition of velocity
. The above definition of velocity  assumes the component form
assumes the component form
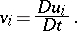 | (a6) |
It may be pointed out that, in solid mechanics, the deformation and motion are generally described in terms of the displacement vector. In fluid mechanics, the motion is generally described in terms of the velocity vector. When a motion is described in terms of velocity, it is commonly referred to as a flow.
Since  is a function of
is a function of 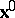 and
and  by definition, the material derivative of
by definition, the material derivative of  , namely,
, namely, 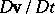 , can be defined. This derivative is called the acceleration of the particle
, can be defined. This derivative is called the acceleration of the particle 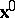 at time
at time 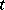 . One often writes
. One often writes 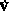 for
for  . Thus, the acceleration of a particle at time
. Thus, the acceleration of a particle at time 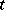 is the rate of change of velocity of that particle at time
is the rate of change of velocity of that particle at time 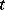 . The components of the acceleration are denoted by
. The components of the acceleration are denoted by 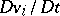 or
or 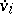 .
.
It is to be emphasized that the velocity and acceleration are defined with reference to a particle and are basically functions of 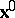 and
and 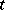 . In the spatial description of motion,
. In the spatial description of motion, 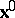 is a function of
is a function of  and
and 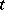 . Hence, like the displacement, velocity and acceleration can also be expressed as functions of
. Hence, like the displacement, velocity and acceleration can also be expressed as functions of  and
and  . When
. When  is expressed as a function of
is expressed as a function of  and
and 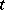 ,
, 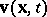 is referred to as the instantaneous velocity at the point
is referred to as the instantaneous velocity at the point  . This actually means that
. This actually means that 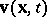 is the velocity at time
is the velocity at time 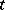 of the particle currently located at the point
of the particle currently located at the point  . Similar terminology is used in respect of acceleration also.
. Similar terminology is used in respect of acceleration also.
Next, one can deduce a formula enabling one to compute the instantaneous acceleration from the instantaneous velocity.
Material derivative in spatial form.
Consider again the function  for which the local derivative was defined by (a2). This function can be expressed as a function of
for which the local derivative was defined by (a2). This function can be expressed as a function of  and
and 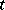 , as explicitly indicated in the following:
, as explicitly indicated in the following:
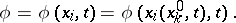 | (a7) |
Consequently, the material derivative of 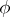 can also be defined. By the chain rule of partial differentiation, we obtain from (a7)
can also be defined. By the chain rule of partial differentiation, we obtain from (a7)
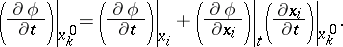 | (a8) |
In view of (a1), (a2) and (a4), it follows that
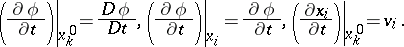 | (a9) |
Hence, denoting 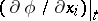 as just
as just 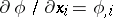 , (a8) can be rewritten as
, (a8) can be rewritten as
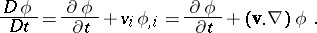 | (a10) |
When  is known as a function of
is known as a function of  and
and 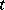 , expression (a10) enables one to compute
, expression (a10) enables one to compute 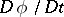 as a function of
as a function of  and
and 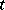 . As such, (a10) serves as a formula for the material derivative in the spatial form. Note that the first term on the right-hand side of this formula, namely
. As such, (a10) serves as a formula for the material derivative in the spatial form. Note that the first term on the right-hand side of this formula, namely 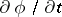 , represents the local rate of change of
, represents the local rate of change of 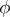 , and the second term, namely
, and the second term, namely  , is the contribution due to the motion. The second term is referred to as the convective rate of change of
, is the contribution due to the motion. The second term is referred to as the convective rate of change of  .
.
It can be easily verified that the material derivative operator
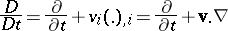 | (a11) |
which operates on functions represented in spatial form, satisfies all the rules of partial differentiation.
The concept of the material derivative and formula (a11) are attributed to L. Euler (1770) and J. Lagrange (1783).
Acceleration in spatial form.
Taking 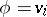 in (a10) gives the following expression for the acceleration:
in (a10) gives the following expression for the acceleration:
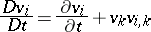 | (a12) |
or, equivalently,
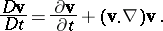 | (a13) |
When  is known as a function of
is known as a function of  and
and 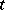 , expression (a13) determines
, expression (a13) determines 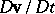 directly in terms of
directly in terms of  and
and  ; this expression therefore serves as a formula for acceleration in the spatial form.
; this expression therefore serves as a formula for acceleration in the spatial form.
By using the standard vector identity, (a13) can be put in the following useful form:
 | (a14) |
From (a13) and (a14), one notes that the acceleration vector is made up of two parts, namely,
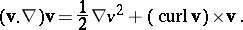 |
Evidently, the second part is quadratically non-linear in nature. Thus, the acceleration depends quadratically on the velocity field, and a given motion cannot be viewed as a superposition of two independent motions in general.
References
| [a1] | D.S. Chandrasekhariah, L. Debnath, "Continuum mechanics" , Acad. Press (1994) |
| [a2] | Y.C. Fung, "Foundations of solid mechanics" , Prentice-Hall (1965) |
Material derivative method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Material_derivative_method&oldid=18473