Winograd small convolution algorithm
A general strategy for computing linear and cyclic convolutions by applying the polynomial version of the Chinese remainder theorem [a1]. For polynomials  and
and  of degree
of degree  and
and  , respectively, the linear convolution
, respectively, the linear convolution
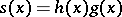 |
has degree  , where
, where  . For any polynomial
. For any polynomial  of degree
of degree  , the linear convolution
, the linear convolution  can be computed by computing the product
can be computed by computing the product  modulo
modulo  , i.e.,
, i.e.,
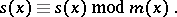 |
The Chinese remainder theorem permits this computation to be localized. Choose a factorization
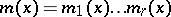 |
into relatively prime factors. The Winograd small convolution algorithm proceeds by first computing the reduced polynomials
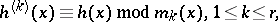 |
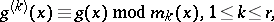 |
followed by the local computations
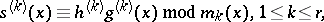 |
and is completed by combining these local computations using the formula
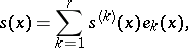 |
where
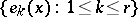 |
is a complete system of idempotents corresponding to the initial factorization of 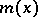 .
.
S. Winograd [a2] expanded on this general strategy by developing bilinear algorithms for computing the product of polynomials modulo a polynomial. Within this general strategy, these bilinear algorithms permit one to use small efficient algorithms as building blocks for larger-size algorithms [a3].
References
| [a1] | A. Borodin, I. Munro, "Computational complexity and algebraic and numeric problems" , Amer. Elsevier (1975) |
| [a2] | S. Winograd, "Some bilinear forms whose multiplicative complexity depends on the field of constants" Math. Systems Th. , 10 (1977) pp. 169–180 |
| [a3] | R.C. Agarwal, J.W. Cooley, "New algorithms for digital convolution" IEEE Trans. Acoustics, Speech and Signal Processing , 25 (1977) pp. 392–410 |
Winograd small convolution algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Winograd_small_convolution_algorithm&oldid=18458