Induction axiom

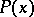The assertion of the validity for all of some predicate defined on the set of all non-negative integers, if the following two conditions hold: 1) 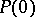is valid; and 2) for any , the truth of 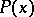implies that of 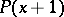. The induction axiom is written in the form

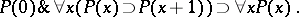In applications of the induction axiom, is called the induction predicate, or the induction proposition, and is called the induction variable, induction parameter or the variable with respect to which the induction is carried out (in those cases when 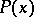contains other parameters apart from ). Here the verification of condition 1) is called the basis of the induction, while the verification of condition 2) is called the induction step. The assumption in 2) of the validity of 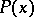, from which is then deduced, is called the induction hypothesis. The principle of (mathematical) induction in mathematics is the scheme of all induction axioms for all possible predicates 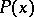. In the system 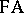of formal arithmetic (cf. Arithmetic, formal), the induction scheme consists merely of those induction axioms that correspond to predicates expressible in 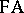(these predicates form a countable set). It is this circumstance, namely the impossibility of expressing in 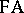induction in its full extent, that is responsible for the incompleteness of 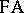(see Gödel incompleteness theorem).

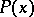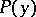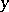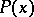Sometimes one considers the following axiom instead of the induction axiom: Let be some property of non-negative integers; if for any it follows from the assumption that is true for all smaller than that is true, then 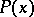is true for all . In other words,

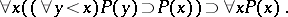This axiom is called the complete or recursive induction axiom. The principle of complete induction is equivalent to the principle of ordinary induction. See also Transfinite induction.

References

[1]	S.C. Kleene, "Mathematical logic" , Wiley (1967)