Sperner property

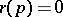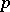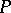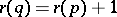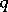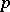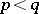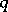Let be a finite partially ordered set (abbreviated: poset) which possesses a rank function , i.e. a function such that for some minimal element of and whenever covers , i.e. and there is no element between and . Let 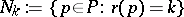be its 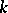th level and let 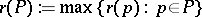be the rank of .

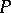An anti-chain or Sperner family in 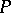is a subset of pairwise incomparable elements of 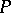. Obviously, each level is an anti-chain. The width (Dilworth number or Sperner number) of 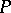is the maximum size 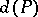of an anti-chain of 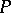. The poset 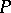is said to have the Sperner property if 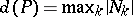. E. Sperner proved in 1928 the Sperner property for Boolean lattices (cf. also Sperner theorem).

More generally, a -family, , is a subset of 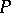containing no chain of 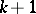elements in 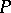, and 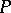has the strong Sperner property if for each 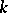the largest size of a 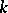-family in 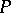equals the largest size of a union of 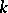levels. There exist several classes of posets having the strong Sperner property:

LYM posets, i.e. posets 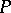satisfying the LYM inequality (cf. also Sperner theorem)

for every anti-cha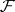in in 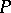or, equivalently,

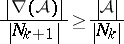for all 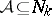, , 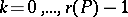where 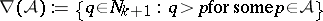. This equivalent property is called the normalized matching property of .

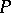Symmetric chain orders, i.e. ranked posets 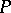which can be decomposed into chains of the form 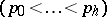where 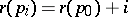, , 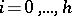and .

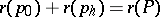Peck posets, i.e. ranked posets 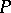such that for all 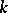and there is a linear operator on the vector space having the basis 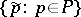with the following properties:

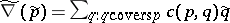with some numbers ,

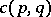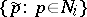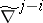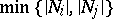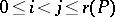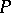the subspace generated by is mapped via to a subspace of dimension for all . If and 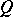are posets from one class, then also the direct product 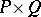(ordered componentwise) belongs to that class, where in the case of LYM posets an additional condition must be supposed: 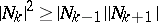for all 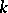(so-called logarithmic concavity). Moreover, quotient theorems have been proved for LYM posets with weight functions and Peck posets.

Every LYM poset with the symmetry and unimodality property 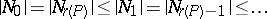is a symmetric chain order and every symmetric chain order is a Peck poset.

Standard examples of posets belonging to all these three classes are the lattice of subsets of a finite set, ordered by inclusion (the Boolean lattice), the lattice of divisors of a natural number, ordered by divisibility, the lattice of all subspaces of an -dimensional vector space over a finite field, ordered by inclusion. The poset of faces of an -dimensional cube, ordered by inclusion, belongs only to the class of LYM posets. The lattice of partitions of a finite set, ordered by refinement, even does not have the Sperner property if is sufficiently large.

Details can be found in [a1].

References

[a1]	K. Engel, "Sperner theory" , Cambridge Univ. Press (1997)