Cohomology group

of a cochain complex 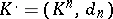of Abelian groups

The graded group 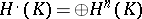, where 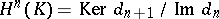(see Complex). The group 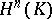is called the -dimensional, or the -th, cohomology group of the complex 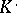. This concept is dual to that of homology group of a chain complex (see Homology of a complex).

In the category of modules, the cohomology module of a cochain complex is also called a cohomology group.

The cohomology group of a chain complex 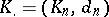of 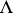-modules with coefficients, or values, in 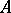, where 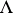is an associative ring with identity and 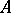is a 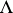-module, is the cohomology group

of the cochain complex

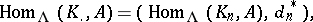where 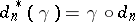, 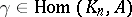. A special case of this construction is the cohomology group of a polyhedron, the singular cohomology group of a topological space, and the cohomology groups of groups, algebras, etc.

If 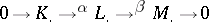is an exact sequence of complexes of -modules, where the images of the 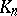are direct factors in 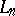, the following exact sequence arises in a natural way:

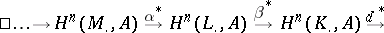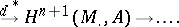On the other hand, if 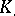is a complex of 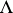-modules, and all 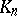are projective, then with every exact sequence 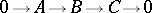of 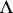-modules is associated an exact sequence of cohomology groups:

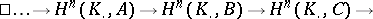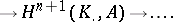See Homology group; Cohomology (for the cohomology group of a topological space).

References

[1]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[2]	R. Godement, "Topologie algébrique et théorie des faisceaux" , Hermann (1958)
[3]	S. MacLane, "Homology" , Springer (1963)

Comments

The exact sequence of cohomology groups given above is often referred to as a long exact sequence of cohomology groups associated to a short exact sequence of complexes.