A solution of the Hermite equation
The Hermite functions have the form
where  is the contour in the complex
is the contour in the complex  -plane consisting of the rays
-plane consisting of the rays  and
and 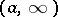 and the semi-circle
and the semi-circle  ,
,  , and
, and 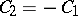 . The half-sum of these solutions,
. The half-sum of these solutions,
for an integer 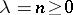 , is equal to the Hermite polynomial
, is equal to the Hermite polynomial 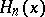 (cf. Hermite polynomials). The name Hermite equation is also used for
(cf. Hermite polynomials). The name Hermite equation is also used for
When  is an integer, this equation has the fundamental system of solutions
is an integer, this equation has the fundamental system of solutions 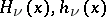 , where
, where 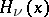 are the Hermite polynomials and
are the Hermite polynomials and  are the Hermite functions of the second kind, which can be expressed in terms of the confluent hypergeometric function:
are the Hermite functions of the second kind, which can be expressed in terms of the confluent hypergeometric function:
References
| [1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 1 , Interscience (1953) (Translated from German) |
| [2] | A. Krazer, W. Franz, "Transzendente Funktionen" , Akademie Verlag (1960) |
The Hermite functions 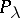 and
and 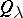 are related to the parabolic cylinder functions (cf. Parabolic cylinder function). See [a1], Sect. 4b for some further results concerning the functions
are related to the parabolic cylinder functions (cf. Parabolic cylinder function). See [a1], Sect. 4b for some further results concerning the functions 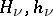 when
when  is a non-negative integer.
is a non-negative integer.
References
| [a1] | L. Durand, "Nicholson-type integrals for products of Gegenbauer functions and related topics" R.A. Askey (ed.) , Theory and Application of Special Functions , Acad. Press (1975) pp. 353–374 |
How to Cite This Entry:
Hermite function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermite_function&oldid=18370
This article was adapted from an original article by M.V. Fedoryuk (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article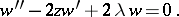
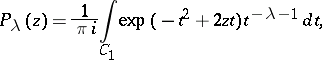
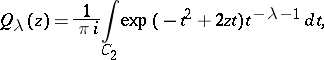
 is the contour in the complex
is the contour in the complex  -plane consisting of the rays
-plane consisting of the rays  and
and 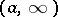 and the semi-circle
and the semi-circle  ,
,  , and
, and 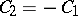 . The half-sum of these solutions,
. The half-sum of these solutions,
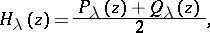
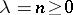 , is equal to the Hermite polynomial
, is equal to the Hermite polynomial 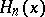 (cf. Hermite polynomials). The name Hermite equation is also used for
(cf. Hermite polynomials). The name Hermite equation is also used for
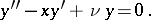
 is an integer, this equation has the fundamental system of solutions
is an integer, this equation has the fundamental system of solutions 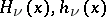 , where
, where 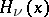 are the Hermite polynomials and
are the Hermite polynomials and  are the Hermite functions of the second kind, which can be expressed in terms of the confluent hypergeometric function:
are the Hermite functions of the second kind, which can be expressed in terms of the confluent hypergeometric function:
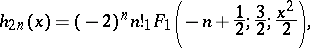
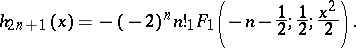
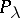 and
and 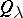 are related to the parabolic cylinder functions (cf. Parabolic cylinder function). See [a1], Sect. 4b for some further results concerning the functions
are related to the parabolic cylinder functions (cf. Parabolic cylinder function). See [a1], Sect. 4b for some further results concerning the functions 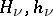 when
when  is a non-negative integer.
is a non-negative integer.