Tolerance intervals
Random intervals, constructed for independent identically-distributed random variables with unknown distribution function 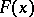 , containing with given probability
, containing with given probability 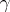 at least a proportion
at least a proportion 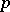 (
( ) of the probability measure
) of the probability measure 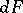 .
.
Let 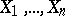 be independent and identically-distributed random variables with unknown distribution function
be independent and identically-distributed random variables with unknown distribution function 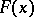 , and let
, and let  ,
, 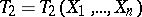 be statistics such that, for a number
be statistics such that, for a number 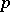 (
(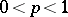 ) fixed in advance, the event
) fixed in advance, the event 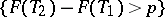 has a given probability
has a given probability 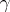 , that is,
, that is,
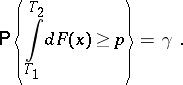 | (1) |
In this case the random interval 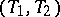 is called a
is called a 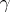 -tolerance interval for the distribution function
-tolerance interval for the distribution function 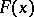 , its end points
, its end points 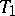 and
and 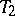 are called tolerance bounds, and the probability
are called tolerance bounds, and the probability 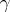 is called a confidence coefficient. It follows from (1) that the one-sided tolerance bounds
is called a confidence coefficient. It follows from (1) that the one-sided tolerance bounds 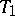 and
and 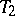 (i.e. with
(i.e. with  , respectively
, respectively 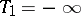 ) are the usual one-sided confidence bounds with confidence coefficient
) are the usual one-sided confidence bounds with confidence coefficient  for the quantiles
for the quantiles 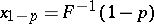 and
and 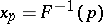 , respectively, that is,
, respectively, that is,
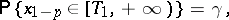 |
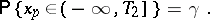 |
Example. Let 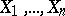 be independent random variables having a normal distribution
be independent random variables having a normal distribution 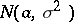 with unknown parameters
with unknown parameters  and
and 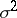 . In this case it is natural to take the tolerance bounds
. In this case it is natural to take the tolerance bounds 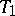 and
and 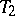 to be functions of the sufficient statistic
to be functions of the sufficient statistic  , where
, where
 |
Specifically, one takes 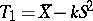 and
and 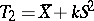 , where the constant
, where the constant 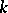 , called the tolerance multiplier, is obtained as the solution to the equation
, called the tolerance multiplier, is obtained as the solution to the equation
 |
where 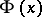 is the distribution function of the standard normal law; moreover,
is the distribution function of the standard normal law; moreover, 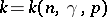 does not depend on the unknown parameters
does not depend on the unknown parameters  and
and 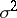 . The tolerance interval constructed in this way satisfies the following property: With confidence probability
. The tolerance interval constructed in this way satisfies the following property: With confidence probability 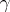 the interval
the interval 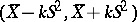 contains at least a proportion
contains at least a proportion 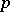 of the probability mass of the normal distribution of the variables
of the probability mass of the normal distribution of the variables 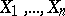 .
.
Assuming the existence of a probability density function 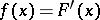 , the probability of the event
, the probability of the event 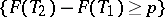 is independent of
is independent of 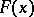 if and only if
if and only if 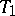 and
and 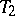 are order statistics (cf. Order statistic). Precisely this fact is the basis of a general method for constructing non-parametric, or distribution-free, tolerance intervals. Let
are order statistics (cf. Order statistic). Precisely this fact is the basis of a general method for constructing non-parametric, or distribution-free, tolerance intervals. Let  be the vector of order statistics constructed from the sample
be the vector of order statistics constructed from the sample 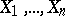 and let
and let
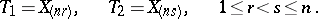 |
Since the random variable 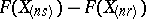 has the beta-distribution with parameters
has the beta-distribution with parameters 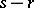 and
and 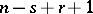 , the probability of the event
, the probability of the event 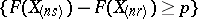 can be calculated as the integral
can be calculated as the integral 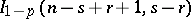 , where
, where 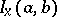 is the incomplete beta-function, and hence in this case instead of (1) one obtains the relation
is the incomplete beta-function, and hence in this case instead of (1) one obtains the relation
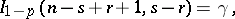 | (2) |
which allows one, for given 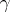 ,
, 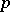 and
and  , to define numbers
, to define numbers  and
and  so that the order statistics
so that the order statistics 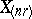 and
and 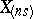 are the tolerance bounds of the desired tolerance interval. Moreover, for given
are the tolerance bounds of the desired tolerance interval. Moreover, for given  ,
,  ,
,  , relation (2) allows one to determine the size
, relation (2) allows one to determine the size  of the collection
of the collection 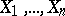 necessary for the relation (2) to hold. There are statistical tables available for solving such problems.
necessary for the relation (2) to hold. There are statistical tables available for solving such problems.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | S.S. Wilks, "Mathematical statistics" , Wiley (1962) |
| [3] | H.H. David, "Order statistics" , Wiley (1981) |
| [4] | R.B. Murphy, "Non-parametric tolerance limits" Ann. Math. Stat. , 19 (1948) pp. 581–589 |
| [5] | P.N. Somerville, "Tables for obtaining non-parametric tolerance limits" Ann. Math. Stat. , 29 (1958) pp. 599–601 |
| [6] | H. Scheffé, J.W. Tukey, "Non-parametric estimation I. Validation of order statistics" Ann. Math. Stat. , 16 (1945) pp. 187–192 |
| [7] | D.A.S. Fraser, "Nonparametric methods in statistics" , Wiley (1957) |
| [8] | A. Wald, J. Wolfowitz, "Tolerance limits for a normal distribution" Ann. Math. Stat. , 17 (1946) pp. 208–215 |
| [9] | H. Robbins, "On distribution-free tolerance limits in random sampling" Ann. Math. Stat. , 15 (1944) pp. 214–216 |
Tolerance intervals. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tolerance_intervals&oldid=18366