Abel inequality
From Encyclopedia of Mathematics
An estimate for the sum of products of two numbers. If sets of numbers 
and 
are given such that the absolute values of all sums 
, 
, are bounded by a number 
, i.e. 
, and if either 
or 
, 
, then
 |
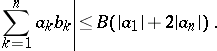If the 
are non-increasing and non-negative, one has the simpler estimate:
 |
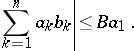Abel's inequality is proved by means of the Abel transformation.
How to Cite This Entry:
Abel inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_inequality&oldid=18342
Abel inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_inequality&oldid=18342
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article