Enumeration theory
The branch of combinatorial analysis in which one examines and develops methods for solving enumeration problems (cf. Enumeration problem). The problems usually amount to counting the number of elements in a finite set having certain properties, or else their equivalence classes. The methods include, for example, the inclusion-and-exclusion principle and various generalizations of it. Pólya's enumeration theory (see Pólya theorem) frequently enables one to overcome difficulties in counting various objects when these are to be considered as indistinguishable. A basic tool in enumeration problems is provided by generating functions (cf. Generating function); they also play an important part in obtaining asymptotic relations (cf. [1]–[3]).
To obtain generating functions in combinatorics considerable use is made of algebras of formal power series and of various symbolic methods (cf. [1], [2], [4]). The basis of the general approach to developing methods for obtaining generating functions is the fact that many discrete objects have a natural order (cf. [1], [5]). In what follows, constructions of incidence algebras are given as examples and it is shown how they enable one to solve certain enumeration problems.
Suppose one is given a partially ordered set  with order relation
with order relation 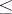 , and suppose that
, and suppose that 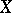 is locally finite, i.e. suppose that any segment
is locally finite, i.e. suppose that any segment
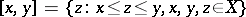 |
of it is finite.
The incidence algebra 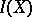 is the set of functions
is the set of functions 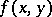 ,
, 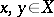 , that take real values and are such that
, that take real values and are such that 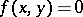 if
if 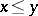 . The sum of two such functions and multiplication by a number are defined in the usual way, while the product
. The sum of two such functions and multiplication by a number are defined in the usual way, while the product 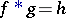 is introduced via
is introduced via
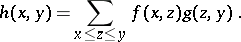 |
Multiplication is associative and distributive with respect to addition. The algebra 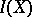 has unit
has unit
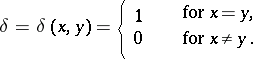 |
Two elements are distinguished in 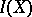 : the zeta-function
: the zeta-function 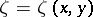 (
(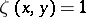 for
for 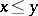 ) and the Möbius function
) and the Möbius function 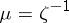 , which is its inverse. The following statement holds: If a locally finite partially ordered set
, which is its inverse. The following statement holds: If a locally finite partially ordered set 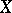 contains its own greatest lower bound, if a function
contains its own greatest lower bound, if a function 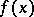 is defined for all
is defined for all 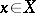 and if
and if 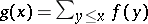 for all
for all 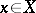 , then for all
, then for all 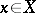 ,
,
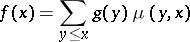 |
(Möbius' inversion theorem).
If 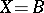 is the set of all finite subsets of a certain countable set, and if
is the set of all finite subsets of a certain countable set, and if 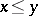 means that
means that 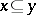 , then for
, then for 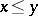 ,
,
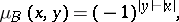 |
and Möbius inversion is simply the inclusion-and-exclusion principle.
If 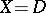 is a set of natural numbers and
is a set of natural numbers and 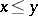 means that
means that  divides
divides 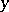 , then for
, then for 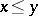 one has
one has 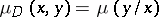 , where
, where 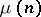 is the number-theoretic Möbius function.
is the number-theoretic Möbius function.
A reduced incidence algebra 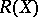 is a subalgebra of
is a subalgebra of 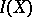 that contains all functions of
that contains all functions of 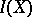 that take equal values on equivalent segments. The relation of segment equivalence has the property that if
that take equal values on equivalent segments. The relation of segment equivalence has the property that if 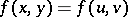 and
and 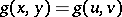 for
for 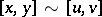 , then also
, then also
 |
This is true, for example, if isomorphic segments are taken as equivalent. The zeta-function and the Möbius function always belong to 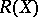 .
.
If 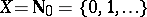 with the natural ordering of numbers, then
with the natural ordering of numbers, then 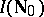 is isomorphic to the algebra of upper-triangular infinite matrices. If
is isomorphic to the algebra of upper-triangular infinite matrices. If 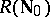 consists of all functions
consists of all functions 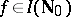 for which
for which 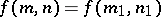 for
for 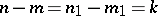 , then the one-to-one relation
, then the one-to-one relation
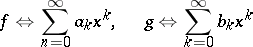 |
holds, where 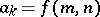 and
and 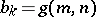 for
for 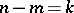 ; thus
; thus
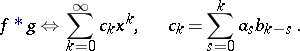 |
Hence 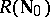 is isomorphic to the algebra of formal power series and
is isomorphic to the algebra of formal power series and
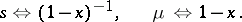 |
If 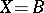 , then
, then 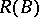 is isomorphic to the algebra of exponential power series
is isomorphic to the algebra of exponential power series
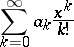 |
and 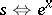 ,
, 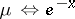 , where
, where 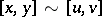 for
for 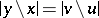 .
.
If 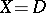 and one considers
and one considers 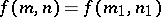 for
for 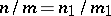 , then
, then 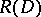 is isomorphic to the algebra of Dirichlet series and
is isomorphic to the algebra of Dirichlet series and
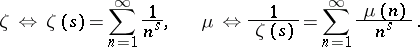 |
Example. Let 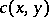 be the number of chains of the form
be the number of chains of the form 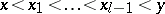 in
in 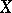 , then
, then 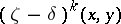 is the number of such chains of length
is the number of such chains of length 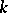 (i.e.
(i.e. 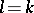 ), hence
), hence
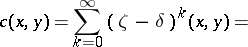 |
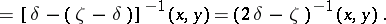 |
Consider this formula in 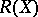 for
for 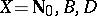 . In the case
. In the case 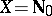 and
and 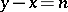 , the number
, the number 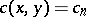 is the number of ordered decompositions (partitions) of
is the number of ordered decompositions (partitions) of  . In
. In 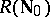 , the formula takes the form
, the formula takes the form
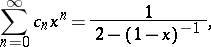 |
hence 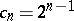 ,
, 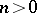 .
.
In the case 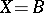 , the number
, the number 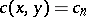 is the number of ordered decompositions of an
is the number of ordered decompositions of an  -element set,
-element set, 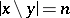 , and
, and
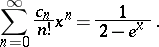 |
In the case 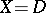 , the number
, the number 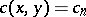 is the number of ordered decompositions of
is the number of ordered decompositions of 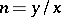 into factors, hence
into factors, hence
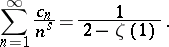 |
References
| [1] | V.N. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian) |
| [2] | J. Riordan, "An introduction to combinational analysis" , Wiley (1958) |
| [3] | , Enumeration problems in combinatorial analysis , Moscow (1979) (In Russian; translated from English) |
| [4] | R. Mullin, G.-C. Rota, "On the foundations of combinatorial theory: III. Theory of binomial enumeration" B. Harris (ed.) , Graph theory and its applications , Acad. Press (1970) pp. 167–213 |
| [5] | G.-C. Rota, "On the foundations of combinatorial theory: I. Theory of Möbius functions" Z. Wahrscheinlichkeitstheor. Verw. Geb. , 2 : 4 (1964) pp. 340–368 |
| [6] | M. Hall, "Combinatorial theory" , Blaisdell (1967) |
Enumeration theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Enumeration_theory&oldid=18324