Gradient dynamical system
A flow (continuous-time dynamical system) given by the gradient of a smooth function 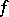 on a smooth manifold. Direct differentiation of
on a smooth manifold. Direct differentiation of 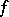 yields a covariant vector (e.g. in the finite-dimensional case in a coordinate neighbourhood
yields a covariant vector (e.g. in the finite-dimensional case in a coordinate neighbourhood 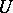 with local coordinates
with local coordinates  this is the vector with components
this is the vector with components 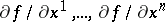 ), while the phase velocity vector is a contravariant vector. The passage from the one to the other is realized with the aid of a Riemannian metric, and the definition of a gradient dynamical system depends on the choice of the metric (as well as on
), while the phase velocity vector is a contravariant vector. The passage from the one to the other is realized with the aid of a Riemannian metric, and the definition of a gradient dynamical system depends on the choice of the metric (as well as on 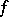 ); the phase velocity vector is often taken with the opposite sign. In the given example the gradient dynamical system in the domain
); the phase velocity vector is often taken with the opposite sign. In the given example the gradient dynamical system in the domain 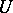 is described by the system of ordinary differential equations
is described by the system of ordinary differential equations
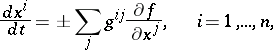 |
where the coefficients 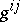 form a matrix inverse to the matrix of coefficients
form a matrix inverse to the matrix of coefficients 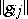 of the metric tensor; it is understood that in all
of the metric tensor; it is understood that in all  equations the right-hand side is taken with the same "plus" or "minus" sign. A gradient dynamical system is often understood to mean a system of a somewhat more general type [1].
equations the right-hand side is taken with the same "plus" or "minus" sign. A gradient dynamical system is often understood to mean a system of a somewhat more general type [1].
References
| [1] | S. Smale, "On gradient dynamical systems" Ann. of Math. (2) , 74 : 1 (1961) pp. 199–206 |
Gradient dynamical system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gradient_dynamical_system&oldid=18305