Split group

over a field 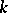, 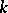-split group

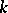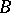A linear algebraic group defined over and containing a Borel subgroup that is split over . Here a connected solvable linear algebraic group is called split over 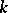if it is defined over 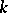and has a composition series (cf. Composition sequence) 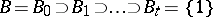such that the 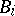are connected algebraic subgroups defined over 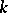and each quotient group 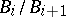is isomorphic over 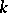to either a one-dimensional torus or to the additive one-dimensional group 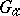. In particular, an algebraic torus is split over 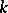if and only if it is defined over 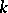and is isomorphic over 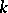to the direct product of copies of the group 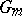. For connected solvable 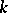-split groups the Borel fixed-point theorem holds. A reductive linear algebraic group defined over 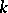is split over if and only if it has a maximal torus split over 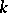, that is, if its 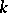-rank coincides with its rank (see Rank of an algebraic group; Reductive group). The image of a 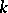-split group under any rational homomorphism defined over 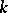is a -split group. Every linear algebraic group 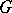defined over a field 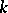is split over an algebraic closure o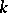f ; if 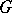is also reductive or solvable and connected, then it is split over some finite extension o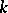f . If 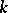is a perfect field, then a connected solvable linear algebraic group defined over 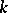is split over 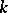if and only if it can be reduced to triangular form over 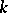. If 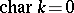, then a linear algebraic group defined over 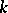is split over 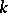if and only if its Lie algebra 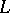is a split (or decomposable) Lie algebra over 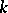; by definition, the latter means that the Lie algebra 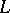has a split Cartan subalgebra, that is, a Cartan subalgebra 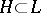for which all eigenvalues of every operator 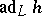, , 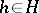belong to .

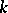If 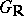is the real Lie group of real points of a semi-simple 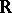-split algebraic group 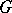and if 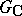is the complexification of the Lie group 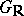, then 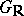is called a normal real form of the complex Lie group .

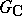There exist quasi-split groups (cf. Quasi-split group) over a field 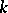that are not split groups over 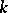; the group 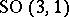is an example for .

References

[1]	A. Borel, "Linear algebraic groups" , Benjamin (1969)
[2]	A. Borel, J. Tits, "Groupes réductifs" Publ. Math. IHES , 27 (1965) pp. 55–150
[3]	Yu.I. Merzlyakov, "Rational groups" , Moscow (1980) (In Russian)
[4]	J.E. Humphreys, "Linear algebraic groups" , Springer (1975)