Number of divisors
From Encyclopedia of Mathematics
A function of a natural argument, 
, equal to the number of natural divisors of the number 
. This arithmetic function is denoted by 
or 
. The following formula holds:
 |
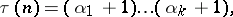where
 |
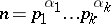is the canonical expansion of 
into prime factors. For prime numbers 
, 
, but there exists an infinite sequence of 
for which
 |
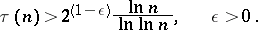On the other hand, for all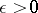 
,
 |
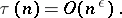is a multiplicative arithmetic function and is equal to the number of points with natural coordinates on the hyperbola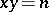 
. The average value of 
is given by Dirichlet's asymptotic formula (cf. Divisor problems). The function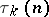 
, which is the number of solutions of the equation 
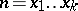in natural numbers 
, is a generalization of the function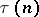 
.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
| [2] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
Comments
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapt. XVI |
How to Cite This Entry:
Number of divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_of_divisors&oldid=18293
Number of divisors. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Number_of_divisors&oldid=18293
This article was adapted from an original article by N.I. Klimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article