Balanced module
From Encyclopedia of Mathematics
A module 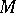 such that the natural ring homomorphism
such that the natural ring homomorphism 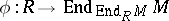 , where
, where 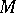 is regarded as a right module over
is regarded as a right module over 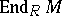 , defined by
, defined by 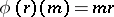 for any
for any 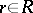 and
and 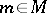 , is surjective. A module
, is surjective. A module 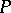 over a ring
over a ring 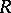 is a generator of the category of
is a generator of the category of  -modules if and only if
-modules if and only if 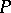 is balanced as an R-module, projective and finitely generated as an
is balanced as an R-module, projective and finitely generated as an 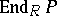 -module.
-module.
References
| [1] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) |
How to Cite This Entry:
Balanced module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balanced_module&oldid=18292
Balanced module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Balanced_module&oldid=18292
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article