Gellerstedt problem
A boundary value problem for a Chaplygin-type equation
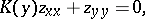 |
in which the function  increases,
increases,  and
and  for
for  . The function
. The function  which is to be found is specified on the boundary. This boundary consists of a sufficiently-smooth contour and pieces of characteristics. This equation is elliptic in the half-plane
which is to be found is specified on the boundary. This boundary consists of a sufficiently-smooth contour and pieces of characteristics. This equation is elliptic in the half-plane  , parabolic on the line
, parabolic on the line  , and hyperbolic for
, and hyperbolic for  . The half-plane of hyperbolicity is covered by two families of characteristics, which satisfy the equations
. The half-plane of hyperbolicity is covered by two families of characteristics, which satisfy the equations  and
and 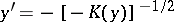 .
.

Figure: g043640a
The characteristics of one of these families merge with the characteristics of the other on the line  .
.
Let 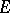 be a simply-connected domain with as boundary a sufficiently-smooth contour
be a simply-connected domain with as boundary a sufficiently-smooth contour 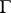 if
if  or pieces
or pieces  ,
,  ,
,  , and
, and 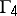 if
if 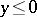 ,
, 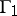 and
and 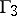 being the characteristics of one family, and
being the characteristics of one family, and  and
and  of the other (see Fig.). The theorem on the existence and the uniqueness of solutions of the following boundary value problems is valid in
of the other (see Fig.). The theorem on the existence and the uniqueness of solutions of the following boundary value problems is valid in  : the function
: the function  is given on
is given on 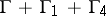 ; the function
; the function  is given on
is given on 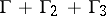 .
.
These problems were first studied (for 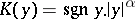 ,
, 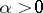 ) by S. Gellerstedt [1] by methods developed by F. Tricomi [2] for the Tricomi problem, and represent a generalization of that problem. Gellerstedt's problem has important applications in gas dynamics with velocities around the velocity of sound. These and related problems were studied for certain multiply-connected domains and for linear equations containing lower-order terms [3].
) by S. Gellerstedt [1] by methods developed by F. Tricomi [2] for the Tricomi problem, and represent a generalization of that problem. Gellerstedt's problem has important applications in gas dynamics with velocities around the velocity of sound. These and related problems were studied for certain multiply-connected domains and for linear equations containing lower-order terms [3].
References
| [1] | S. Gellerstedt, "Quelques problèmes mixtes pour l'équation  " Ark. Mat. Astr. Fysik , 26A : 3 (1937) pp. 1–32 " Ark. Mat. Astr. Fysik , 26A : 3 (1937) pp. 1–32 |
| [2] | F.G. Tricomi, "Integral equations" , Interscience (1957) |
| [3] | M.M. Smirnov, "Equations of mixed type" , Amer. Math. Soc. (1978) (Translated from Russian) |
Comments
References
| [a1] | L. Bers, "Mathematical aspects of subsonic and transonic gas dynamics" , Wiley (1958) |
Gellerstedt problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gellerstedt_problem&oldid=18287