Riemann sphere
A sphere in the Euclidean space 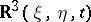 onto which the extended complex plane
onto which the extended complex plane 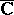 is conformally and one-to-one transformed under stereographic projection. For example, the unit sphere
is conformally and one-to-one transformed under stereographic projection. For example, the unit sphere
 |
can be taken as the Riemann sphere and the plane 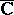 can be identified with the plane
can be identified with the plane 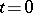 such that the real axis coincides with the axis
such that the real axis coincides with the axis 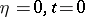 and the imaginary axis with the axis
and the imaginary axis with the axis 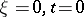 (see Fig.).
(see Fig.).
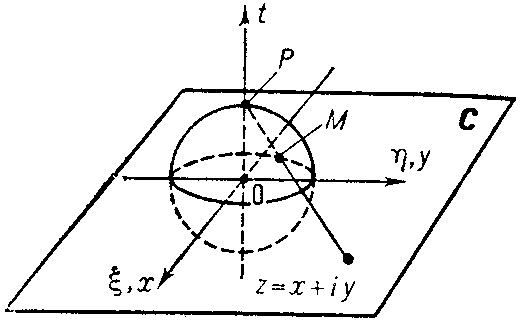
Figure: r082010a
Under stereographic projection to each point 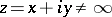 there corresponds the point
there corresponds the point 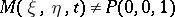 obtained as the point of intersection of the ray drawn from the north pole of the sphere,
obtained as the point of intersection of the ray drawn from the north pole of the sphere, 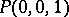 , to the point
, to the point  with the sphere
with the sphere 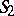 ; the north pole
; the north pole 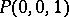 corresponds to the point at infinity,
corresponds to the point at infinity, 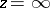 . Analytically this relation can be expressed by the formulas
. Analytically this relation can be expressed by the formulas
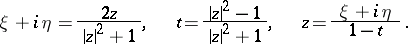 | (*) |
In other words, the correspondence (*) determines a differentiable imbedding of the one-dimensional complex projective space 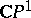 into the space
into the space 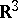 in the form of the sphere
in the form of the sphere 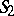 . In many questions of the theory of functions, the extended complex plane is identified with the Riemann sphere. The exclusive role of the point at infinity of the plane
. In many questions of the theory of functions, the extended complex plane is identified with the Riemann sphere. The exclusive role of the point at infinity of the plane 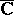 may be dispensed with if the distance between two points
may be dispensed with if the distance between two points 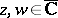 is taken to be the chordal, or spherical, distance
is taken to be the chordal, or spherical, distance 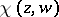 between their images
between their images  :
:
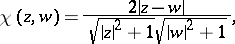 |
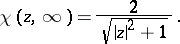 |
A higher-dimensional complex projective space 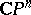 ,
,  , can be imbedded into the space
, can be imbedded into the space 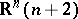 by a complex
by a complex  -dimensional stereographic projection, generalizing the formulas (*) (see [2]).
-dimensional stereographic projection, generalizing the formulas (*) (see [2]).
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [2] | B.A. Fuks, "Introduction to the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) |
Comments
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8 |
Riemann sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Riemann_sphere&oldid=18286