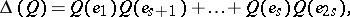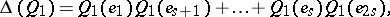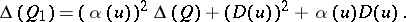A construction used in the study of quadratic forms over fields of characteristic 2, which allows one, in particular, to introduce analogues of the special orthogonal group over such fields. In fact, a Dickson invariant is an element 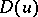 of a field
of a field  of characteristic 2 associated to any similarity
of characteristic 2 associated to any similarity  of a countable-dimensional vector space
of a countable-dimensional vector space 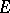 over
over 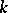 with respect to the symmetric bilinear form
with respect to the symmetric bilinear form 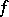 associated with a non-degenerate quadratic form
associated with a non-degenerate quadratic form 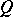 on
on 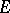 . Introduced by L.E. Dickson [1].
. Introduced by L.E. Dickson [1].
By virtue of the condition imposed on the characteristic of the field, the form 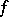 is alternating and there exists a basis
is alternating and there exists a basis 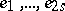 in
in 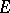 for which
for which
for 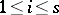 ,
,  (cf. Witt decomposition). Let
(cf. Witt decomposition). Let
for any vectors  and
and 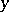 from
from 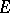 , and let, for each
, and let, for each 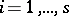 ,
,
Then the following element from 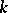 :
:
is called the Dickson invariant of the similarity  with respect to the basis
with respect to the basis 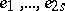 . For
. For  to be a similarity with respect to
to be a similarity with respect to 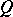 with similarity coefficient
with similarity coefficient  (i.e.
(i.e.  for any vector
for any vector 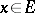 ) it is necessary and sufficient that
) it is necessary and sufficient that 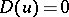 or that
or that 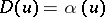 . Similarities
. Similarities  with respect to
with respect to 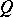 for which
for which 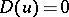 are called direct similarities. The direct similarities form a normal subgroup of index 2 in the group of all similarities with respect to
are called direct similarities. The direct similarities form a normal subgroup of index 2 in the group of all similarities with respect to 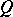 .
.
If  is the form defined by
is the form defined by 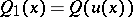 for any vector
for any vector 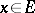 , and if
, and if 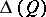 and
and  are the pseudo-discriminants of these forms with respect to the basis
are the pseudo-discriminants of these forms with respect to the basis  , i.e.
, i.e.
then
References
| [1] | L.E. Dickson, "Linear groups" , Teubner (1901) |
| [2] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [3] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
How to Cite This Entry:
Dickson invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dickson_invariant&oldid=18238
This article was adapted from an original article by V.L. Popov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article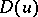 of a field
of a field  of characteristic 2 associated to any similarity
of characteristic 2 associated to any similarity  of a countable-dimensional vector space
of a countable-dimensional vector space 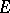 over
over 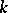 with respect to the symmetric bilinear form
with respect to the symmetric bilinear form 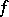 associated with a non-degenerate quadratic form
associated with a non-degenerate quadratic form 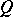 on
on 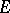 . Introduced by L.E. Dickson [1].
. Introduced by L.E. Dickson [1].
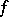 is alternating and there exists a basis
is alternating and there exists a basis 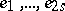 in
in 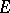 for which
for which
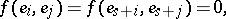
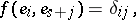
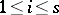 ,
,  (cf. Witt decomposition). Let
(cf. Witt decomposition). Let

 and
and 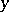 from
from 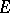 , and let, for each
, and let, for each 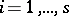 ,
,
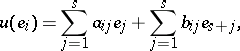

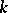 :
:

 with respect to the basis
with respect to the basis 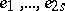 . For
. For  to be a similarity with respect to
to be a similarity with respect to 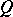 with similarity coefficient
with similarity coefficient  (i.e.
(i.e.  for any vector
for any vector 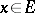 ) it is necessary and sufficient that
) it is necessary and sufficient that 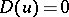 or that
or that 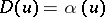 . Similarities
. Similarities  with respect to
with respect to 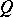 for which
for which 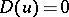 are called direct similarities. The direct similarities form a normal subgroup of index 2 in the group of all similarities with respect to
are called direct similarities. The direct similarities form a normal subgroup of index 2 in the group of all similarities with respect to 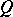 .
.
 is the form defined by
is the form defined by 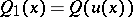 for any vector
for any vector 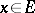 , and if
, and if 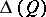 and
and  are the pseudo-discriminants of these forms with respect to the basis
are the pseudo-discriminants of these forms with respect to the basis  , i.e.
, i.e.