Hellinger integral
From Encyclopedia of Mathematics
An integral of Riemann type of a set function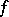 
. If 
is a space with a finite, non-negative, non-singular measure; if 
, 
, is a totally-additive function with 
for 
; and if 
is a partition of 
, then
 |
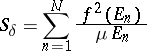and the Hellinger integral of 
with respect to 
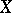is defined as
 |
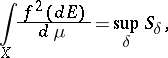provided that this supremum is finite. Hellinger's integral can also be regarded as the limit over a directed set of partitions: 
if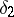 
is a subdivision of 
.
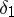If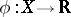 
is a summable function such that 
is the Lebesgue integral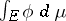 
, then the Hellinger integral can be expressed in terms of the Lebesgue integral:
 |
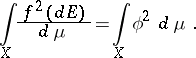E. Hellinger in [1] defined the integral for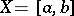 
in terms of point functions.
References
| [1] | E. Hellinger, "Neue Begründung der Theorie quadratischer Formen von unendlichvielen Veränderlichen" J. Reine Angew. Math. , 136 (1909) pp. 210–271 |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian) |
How to Cite This Entry:
Hellinger integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hellinger_integral&oldid=18237
Hellinger integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hellinger_integral&oldid=18237
This article was adapted from an original article by I.A. Vinogradova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article