Fractional power
of a linear operator 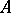 on a complex Banach space
on a complex Banach space 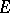
A function  of this operator such that
of this operator such that  . If the operator
. If the operator  is bounded and its spectrum does not contain zero and does not surround it,
is bounded and its spectrum does not contain zero and does not surround it, 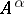 is defined by a Cauchy integral along a contour around the spectrum of
is defined by a Cauchy integral along a contour around the spectrum of 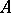 not containing zero. If
not containing zero. If 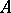 is unbounded, the contour has to be taken infinite, and problems on the convergence of the integral arise. If
is unbounded, the contour has to be taken infinite, and problems on the convergence of the integral arise. If 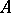 has a domain of definition
has a domain of definition 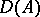 which is dense in
which is dense in 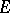 , and has for
, and has for 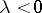 a resolvent
a resolvent
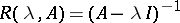 |
satisfying the estimate
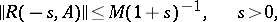 | (1) |
then
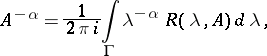 |
where  consists of the sides of an angle depending on
consists of the sides of an angle depending on 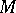 . The operators
. The operators 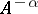 are bounded and
are bounded and 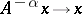 for any
for any  as
as  . Positive powers are defined as follows:
. Positive powers are defined as follows: 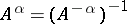 ; they are unbounded. For any real
; they are unbounded. For any real 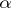 and
and 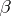 the following fundamental property of powers holds:
the following fundamental property of powers holds:
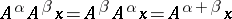 |
for 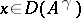 and
and  . If
. If 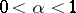 ,
, 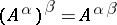 . For any
. For any 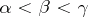 and
and 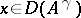 ,
,
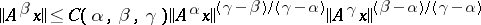 |
(inequality of moments). The power semi-group 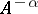 permits extension to the semi-group
permits extension to the semi-group 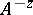 which is analytic in the right half-plane.
which is analytic in the right half-plane.
The above properties are extended to include the case when 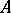 has no bounded inverse and when the estimate
has no bounded inverse and when the estimate 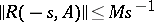 ,
, 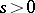 , holds. If condition (1) is met and if
, holds. If condition (1) is met and if 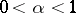 , then
, then
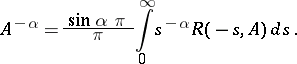 |
If 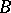 is the infinitesimal operator of a contraction semi-group
is the infinitesimal operator of a contraction semi-group 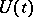 , then
, then
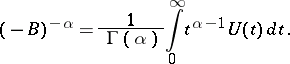 |
It does not follow from condition (1) that 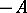 is the infinitesimal operator of a strongly-continuous semi-group, but the operator
is the infinitesimal operator of a strongly-continuous semi-group, but the operator 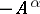 is the infinitesimal operator of an analytic semi-group if
is the infinitesimal operator of an analytic semi-group if 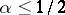 .
.
An operator 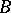 is dominated by an operator
is dominated by an operator 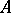 if
if 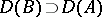 and if
and if 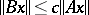 ,
, 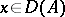 . If
. If 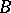 is dominated by
is dominated by 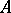 and if the resolvents of both operators have the property (1), then
and if the resolvents of both operators have the property (1), then  is dominated by
is dominated by 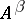 if
if 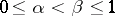 .
.
If 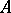 is a positive self-adjoint operator on a Hilbert space, its fractional power is defined by the spectral decomposition (cf. Spectral decomposition of a linear operator):
is a positive self-adjoint operator on a Hilbert space, its fractional power is defined by the spectral decomposition (cf. Spectral decomposition of a linear operator):
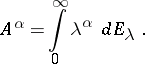 |
In the inequality of moments, 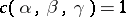 for such an operator. Let
for such an operator. Let 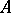 and
and 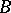 be two positive self-adjoint operators, acting on Hilbert spaces
be two positive self-adjoint operators, acting on Hilbert spaces 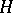 and
and 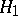 , respectively. If
, respectively. If 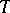 is a bounded linear operator from
is a bounded linear operator from  to
to 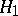 with norm
with norm 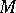 such that
such that 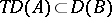 and
and 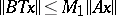 ,
, 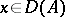 , then
, then 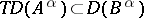 and
and
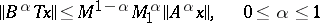 |
(Heinz's inequality). In particular, if 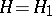 and
and  , the fact that
, the fact that 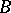 is dominated by
is dominated by 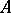 implies that
implies that 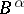 is dominated by
is dominated by 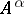 if
if 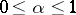 . Fractional powers of operators are employed in the study of non-linear equations. They have been studied in detail for operators generated by elliptic boundary value problems.
. Fractional powers of operators are employed in the study of non-linear equations. They have been studied in detail for operators generated by elliptic boundary value problems.
References
| [1] | S.G. Krein (ed.) , Functional analysis , Wolters-Noordhoff (1972) (Translated from Russian) |
| [2] | S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) |
| [3] | R.T. Seeley, "Complex powers of elliptic operators" , Proc. Symp. Pure Math. , 10 , Amer. Math. Soc. (1967) pp. 288–307 |
Comments
References
| [a1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
Fractional power. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fractional_power&oldid=18216