Orbit method

A method for studying unitary representations of Lie groups. The theory of unitary representations (cf. Unitary representation) of nilpotent Lie groups was developed using the orbit method, and it has been shown that this method can also be used for other groups (see [1]).

The orbit method is based on the following "experimental" fact: A close connection exists between unitary irreducible representations of a Lie group 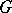and its orbits in the coadjoint representation. The solution of basic problems in the theory of representations using the orbit method is achieved in the following way (see [2]).

Construction and classification of irreducible unitary representations.

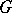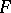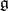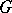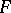Let be an orbit of a real Lie group in the coadjoint representation, let be a point of this orbit (which is a linear functional on the Lie algebra of ), let be the stabilizer of , and let 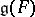be the Lie algebra of the group 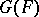. A complex subalgebra 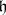in 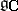is called a polarization of the point 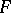( 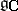is the complexification of the Lie algebra 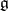, cf. Complexification of a Lie algebra) if and only if it possesses the following properties:

1) ;

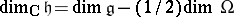2) 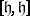is contained in the kernel of the functional 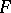on ;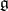

3) 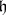is invariant with respect to .

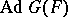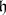Let and . The polarization is called real if 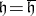and purely complex if 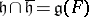. The functional 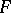defines a character (a one-dimensional unitary representation) 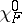of the group 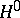according to the formula

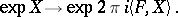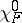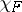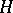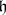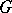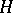Extend to a character of . If is a real polarization, then let be the representation of the group induced by the character of the subgroup (see Induced representation). If 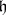is a purely complex polarization, then let 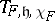be the holomorphically induced representation operating on the space of holomorphic functions on .

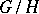The first basic hypothesis is that the representation 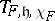is irreducible (cf. Irreducible representation) and its equivalence class depends only on the orbit and the choice of the extension 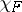of the character 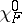. This hypothesis is proved for nilpotent groups [1] and for solvable Lie groups [5]. For certain orbits of the simple special group 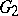the hypothesis does not hold [7]. The possibility of an extension and its degree of ambiguity depend on topological properties of the orbit: -dimensional cohomology classes act as obstacles to the extension, while 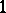-dimensional cohomology classes of the orbit can be used as a parameter for enumerating different extensions. More precisely, let 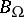be a canonical -form on the orbit . For an extension to exist, it is necessary and sufficient that 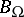belongs to the integer homology classes (i.e. that its integral along any -dimensional cycle is an integer); if this condition is fulfilled, then the set of extensions is parametrized by the characters of the fundamental group of the orbit.

The second basic hypothesis is that all unitary irreducible representations of the group 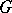in question are obtained in the way shown. Up to 1983, the only examples which contradicted this hypothesis were the so-called complementary series of representations of semi-simple Lie groups.

Functional properties of the relation between orbits and representations.

In the theory of representations great significance is attached to questions of decomposition into irreducible components of a representation: Given a subgroup 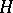of a group 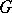, how are such decompositions obtained by restricting an irreducible representation of 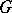to 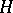and by inducing an irreducible representation of 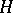to 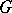? The orbit method gives answers to these questions in terms of a natural projection (where signifies a transfer to the adjoint space; the projection 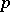consists of restriction of a functional from 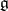onto 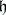). Indeed, let 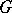be an exponential Lie group (for such groups the relation between orbits and representations is a one-to-one relation, cf. Lie group, exponential). The irreducible representation of 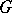corresponding to the orbit 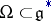, when restricted to 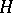, decomposes into irreducible components corresponding to those orbits 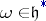which ly in 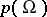, while a representation of 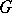induced by an irreducible representation of the group 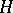, corresponding to the orbit 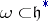, decomposes into irreducible components corresponding to the orbits 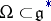which have a non-empty intersection with the pre-image . These results have two important consequences: If the irreducible representations 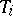correspond to the orbits 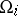, , 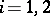then the tensor product 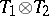decomposes into irreducible components corresponding to those orbits which ly in the arithmetic sum 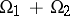; a quasi-regular representation of 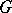in a space of functions on 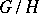decomposes into irreducible components corresponding to those orbits 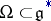for which the image 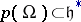contains zero.

Character theory.

For characters of irreducible representations (as generalized functions on a group) the following universal formula has been proposed (see [2]):

(*)

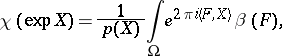where 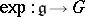is the exponential mapping of the Lie algebra 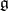into the group 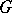, where 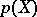is the square root of the density of the invariant Haar measure on 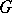in canonical coordinates and where 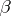is the volume form on the orbit connected to the canonical -form 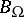by the relation 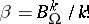, 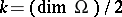. This formula is correct for nilpotent groups, solvable groups of type 1, compact groups, discrete series of representations of semi-simple real groups, and principal series of representations of complex semi-simple groups. For certain degenerate series of representations of 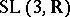the formula does not hold. 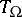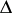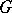Formula (*) provides a simple formula for the calculation of the infinitesimal character of the irreducible representation corresponding to the orbit ; moreover, to each Laplace operator on an 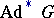-invariant polynomial 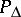on 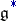is related, such that the value of the infinitesimal character of the representation 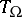at the element 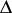is equal to the value of 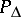at .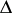

Construction of an irreducible unitary representation of the group 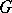along its orbit in the coadjoint representation.

This construction can be considered as a quantization operation of a Hamiltonian system for which plays the role of phase space, while 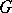plays the role of a multi-dimensional non-commutative time (or group of symmetries). Under these conditions, the 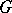-orbits in the coadjoint representation are all 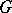-homogeneous symplectic manifolds which admit quantization. The second basic hypothesis can therefore be reformulated thus: Every elementary quantum system with time (or group of symmetries) 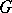is obtained by quantization from the corresponding classical system (see [2]).

A connection has also been discovered with the theory of completely-integrable Hamiltonian systems (see [11]).

References

[1]	A.A. Kirillov, "Unitary representations of nilpotent Lie groups" Russian Math. Surveys , 17 : 4 (1962) pp. 53–104 Uspekhi Mat. Nauk , 17 : 4 (1962) pp. 57–110
[2]	A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian)
[3]	J. Dixmier, "Enveloping algebras" , North-Holland (1974) (Translated from French)
[4]	D.J. Simms, N.M.J. Woodhouse, "Lectures on geometric quantization" , Springer (1976)
[5]	L. Auslander, B. Kostant, "Polarization and unitary representations of solvable Lie groups" Invent. Math. , 14 (1971) pp. 255–354
[6]	C.C. Moore, "Decomposition of unitary representations defined by discrete subgroups of nilpotent groups" Ann. of Math. , 82 : 1 (1965) pp. 146–182
[7]	L.P. Rothschild, J.A. Wolf, "Representations of semisimple groups associated to nilpotent orbits" Ann. Sci. Ecole Norm. Sup. Ser. 4 , 7 (1974) pp. 155–173
[8]	P. Bernal, et al., "Représentations des groupes de Lie résolubles" , Dunod (1972)
[9]	V.A. Ginzburg, "The method of orbits and perturbation theory" Soviet Math. Dokl. , 20 : 6 (1979) pp. 1287–1291 Dokl. Akad. Nauk SSSR , 249 : 3 (1979) pp. 525–528
[10]	A.A. Kirillov, "Infinite dimensional groups, their representations, orbits, invariants" , Proc. Internat. Congress Mathematicians (Helsinki, 1978) , 2 , Acad. Sci. Fennicae (1980) pp. 705–708
[11]	A.G. Reyman, M.A. Semenov-Tian-Shansky, "Reduction of Hamiltonian systems, affine Lie algebras and Lax equations" Invent. Math. , 54 : 1 (1979) pp. 81–100
[12]	A.A. Kirillov, "Introduction to representation theory and noncommutative analysis" , Springer (to appear) (Translated from Russian)