Stochastic continuity
From Encyclopedia of Mathematics
A property of the sample functions of a stochastic process. A stochastic process 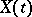 defined on a set
defined on a set 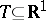 is called stochastically continuous on this set if for any
is called stochastically continuous on this set if for any 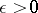 and all
and all 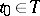 ,
,
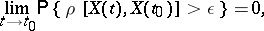 |
where 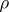 is the distance between points in the corresponding space of values of
is the distance between points in the corresponding space of values of 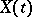 .
.
References
| [1] | Yu.V. [Yu.V. Prokhorov] Prohorov, Yu.A. Rozanov, "Probability theory, basic concepts. Limit theorems, random processes" , Springer (1979) (Translated from Russian) |
How to Cite This Entry:
Stochastic continuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_continuity&oldid=18160
Stochastic continuity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_continuity&oldid=18160
This article was adapted from an original article by A.V. Prokhorov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article