Van der Waerden test
A non-parametric test for the homogeneity of two samples 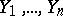 and
and 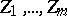 , based on the rank statistic
, based on the rank statistic
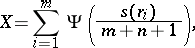 |
where 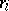 are the ranks (ordinal numbers) of the random variables
are the ranks (ordinal numbers) of the random variables 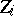 in the series of joint order statistics of
in the series of joint order statistics of 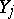 and
and 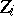 ; the function
; the function 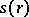 is defined by the pre-selected permutation
is defined by the pre-selected permutation
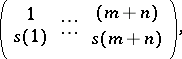 |
and 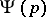 is the inverse function of the normal distribution with parameters
is the inverse function of the normal distribution with parameters 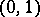 . The permutation is so chosen that for a given alternative hypothesis the test will be the strongest. If
. The permutation is so chosen that for a given alternative hypothesis the test will be the strongest. If 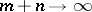 , irrespective of the behaviour of
, irrespective of the behaviour of  and
and  individually, the asymptotic distribution of
individually, the asymptotic distribution of 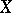 is normal. If
is normal. If  and
and 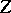 are independent and normally distributed with equal variances, the test for the alternative choice
are independent and normally distributed with equal variances, the test for the alternative choice 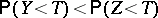 or
or 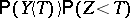 (in this case
(in this case 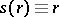 ) is asymptotically equally as strong as the Student test. Introduced by B.L. van der Waerden [1].
) is asymptotically equally as strong as the Student test. Introduced by B.L. van der Waerden [1].
References
| [1] | B.L. van der Waerden, "Order tests for the two-sample problem and their power" Proc. Kon. Nederl. Akad. Wetensch. A , 55 (1952) pp. 453–458 |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
Comments
References
| [a1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1986) |
| [a2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
Van der Waerden test. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Van_der_Waerden_test&oldid=18157