Orthogonal group
The group of all linear transformations of an  -dimensional vector space
-dimensional vector space 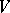 over a field
over a field 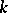 which preserve a fixed non-singular quadratic form
which preserve a fixed non-singular quadratic form 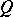 on
on 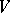 (i.e. linear transformations
(i.e. linear transformations 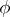 such that
such that 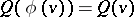 for all
for all 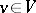 ). An orthogonal group is a classical group. The elements of an orthogonal group are called orthogonal transformations of
). An orthogonal group is a classical group. The elements of an orthogonal group are called orthogonal transformations of 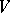 (with respect to
(with respect to 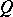 ), or also automorphisms of the form
), or also automorphisms of the form 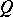 . Furthermore, let
. Furthermore, let 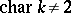 (for orthogonal groups over fields with characteristic 2 see [1], [7]) and let
(for orthogonal groups over fields with characteristic 2 see [1], [7]) and let 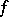 be the non-singular symmetric bilinear form on
be the non-singular symmetric bilinear form on 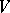 related to
related to 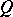 by the formula
by the formula
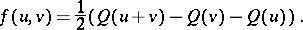 |
The orthogonal group then consists of those linear transformations of 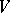 that preserve
that preserve 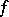 , and is denoted by
, and is denoted by 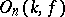 , or (when one is talking of a specific field
, or (when one is talking of a specific field 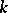 and a specific form
and a specific form 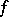 ) simply by
) simply by 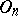 . If
. If 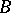 is the matrix of
is the matrix of 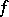 with respect to some basis of
with respect to some basis of 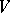 , then the orthogonal group can be identified with the group of all
, then the orthogonal group can be identified with the group of all 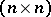 -matrices
-matrices 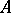 with coefficients in
with coefficients in 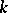 such that
such that 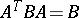 (
(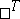 is transposition).
is transposition).
The description of the algebraic structure of an orthogonal group is a classical problem. The determinant of any element from 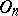 is equal to 1 or
is equal to 1 or 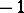 . Elements with determinant 1 are called rotations; they form a normal subgroup
. Elements with determinant 1 are called rotations; they form a normal subgroup 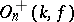 (or simply
(or simply 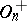 ) of index 2 in the orthogonal group, called the rotation group. Elements from
) of index 2 in the orthogonal group, called the rotation group. Elements from 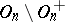 are called inversions. Every rotation (inversion) is the product of an even (odd) number of reflections from
are called inversions. Every rotation (inversion) is the product of an even (odd) number of reflections from 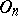 .
.
Let 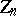 be the group of all homotheties
be the group of all homotheties 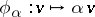 ,
, 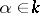 ,
, 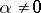 , of the space
, of the space 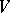 . Then
. Then 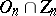 is the centre of
is the centre of 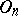 ; it consists of two elements:
; it consists of two elements: 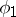 and
and 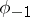 . If
. If  is odd, then
is odd, then 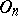 is the direct product of its centre and
is the direct product of its centre and 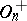 . If
. If 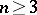 , the centre of
, the centre of 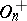 is trivial if
is trivial if  is odd, and coincides with the centre of
is odd, and coincides with the centre of 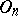 if
if  is even. If
is even. If 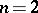 , the group
, the group 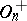 is commutative and is isomorphic either to the multiplicative group
is commutative and is isomorphic either to the multiplicative group 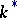 of
of 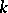 (when the Witt index
(when the Witt index  of
of 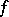 is equal to 1), or to the group of elements with norm 1 in
is equal to 1), or to the group of elements with norm 1 in 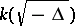 , where
, where 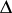 is the discriminant of
is the discriminant of 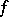 (when
(when 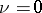 ). The commutator subgroup of
). The commutator subgroup of 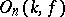 is denoted by
is denoted by 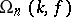 , or simply by
, or simply by 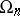 ; it is generated by the squares of the elements from
; it is generated by the squares of the elements from 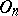 . When
. When 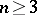 , the commutator subgroup of
, the commutator subgroup of 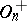 coincides with
coincides with 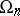 . The centre of
. The centre of 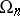 is
is 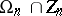 .
.
Other classical groups related to orthogonal groups include the canonical images of 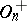 and
and 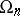 in the projective group; they are denoted by
in the projective group; they are denoted by 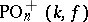 and
and 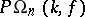 (or simply by
(or simply by 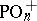 and
and 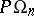 ) and are isomorphic to
) and are isomorphic to 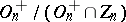 and
and 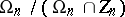 , respectively.
, respectively.
The basic classical facts about the algebraic structure describe the successive factors of the following series of normal subgroups of an orthogonal group:
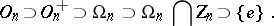 |
The group 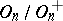 has order 2. Every element in
has order 2. Every element in 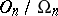 has order 2, thus this group is defined completely by its cardinal number, and this number can be either infinite or finite of the form
has order 2, thus this group is defined completely by its cardinal number, and this number can be either infinite or finite of the form 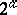 where
where  is an integer. The description of the remaining factors depends essentially on the Witt index
is an integer. The description of the remaining factors depends essentially on the Witt index  of the form
of the form 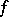 .
.
First, let 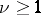 . Then
. Then 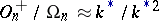 when
when 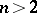 . This isomorphism is defined by the spinor norm, which defines an epimorphism from
. This isomorphism is defined by the spinor norm, which defines an epimorphism from 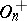 on
on 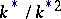 with kernel
with kernel 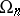 . The group
. The group 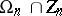 is non-trivial (and consists of the transformations
is non-trivial (and consists of the transformations 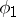 and
and 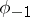 ) if and only if
) if and only if  is even and
is even and 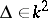 . If
. If 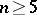 , then the group
, then the group 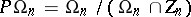 is simple. The cases where
is simple. The cases where 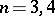 are studied separately. Namely,
are studied separately. Namely, 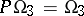 is isomorphic to
is isomorphic to 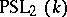 (see Special linear group) and is also simple if
(see Special linear group) and is also simple if 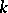 has at least 4 elements (the group
has at least 4 elements (the group 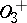 is isomorphic to the projective group
is isomorphic to the projective group 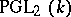 ). When
). When 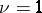 , the group
, the group 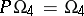 is isomorphic to the group
is isomorphic to the group 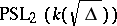 and is simple (in this case
and is simple (in this case 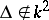 ), while when
), while when 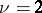 , the group
, the group 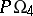 is isomorphic to
is isomorphic to 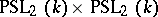 and is not simple. In the particular case when
and is not simple. In the particular case when 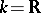 and
and 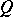 is a form of signature
is a form of signature 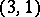 , the group
, the group 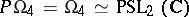 is called the Lorentz group.
is called the Lorentz group.
When 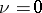 (i.e.
(i.e. 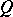 is an anisotropic form), these results are not generally true. For example, if
is an anisotropic form), these results are not generally true. For example, if 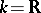 and
and 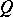 is a positive-definite form, then
is a positive-definite form, then 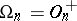 , although
, although 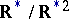 consists of two elements; when
consists of two elements; when 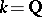 ,
, 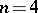 , one can have
, one can have 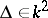 , but
, but 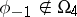 . When
. When 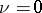 , the structures of an orthogonal group and its related groups essentially depend on
, the structures of an orthogonal group and its related groups essentially depend on 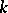 . For example, if
. For example, if 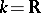 , then
, then 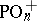 ,
, 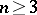 ,
, 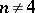 ,
, 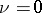 , is simple (and
, is simple (and 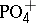 is isomorphic to the direct product
is isomorphic to the direct product 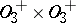 of two simple groups); if
of two simple groups); if 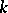 is the field of
is the field of 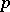 -adic numbers and
-adic numbers and 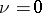 , there exists in
, there exists in 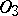 (and
(and 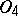 ) an infinite normal series with Abelian quotients. Important special cases are when
) an infinite normal series with Abelian quotients. Important special cases are when 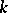 is a locally compact field or an algebraic number field. If
is a locally compact field or an algebraic number field. If 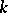 is the field of
is the field of 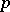 -adic numbers, then
-adic numbers, then 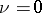 is impossible when
is impossible when 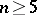 . If
. If 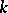 is an algebraic number field, then there is no such restriction and one of the basic results is that
is an algebraic number field, then there is no such restriction and one of the basic results is that 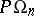 , when
, when 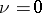 and
and 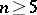 , is simple. In this case, the study of orthogonal groups is closely connected with the theory of equivalence of quadratic forms, where one needs the forms obtained from
, is simple. In this case, the study of orthogonal groups is closely connected with the theory of equivalence of quadratic forms, where one needs the forms obtained from 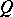 by extension of coefficients to the local fields defined by valuations of
by extension of coefficients to the local fields defined by valuations of 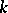 (the Hasse principle).
(the Hasse principle).
If 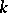 is the finite field
is the finite field 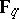 of
of 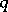 elements, then an orthogonal group is finite. The order of
elements, then an orthogonal group is finite. The order of 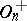 for
for  odd is equal to
odd is equal to
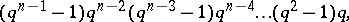 |
while when 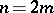 it is equal to
it is equal to
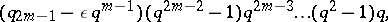 |
where 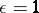 if
if 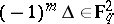 and
and 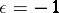 otherwise. These formulas and general facts about orthogonal groups when
otherwise. These formulas and general facts about orthogonal groups when 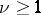 also allow one to calculate the orders of
also allow one to calculate the orders of 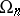 and
and 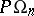 , since
, since 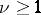 when
when 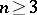 , while the order of
, while the order of 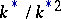 is equal to 2. The group
is equal to 2. The group 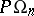 ,
, 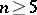 , is one of the classical simple finite groups (see also Chevalley group).
, is one of the classical simple finite groups (see also Chevalley group).
One of the basic results on automorphisms of orthogonal groups is the following: If 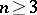 , then every automorphism
, then every automorphism 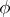 of
of 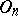 has the form
has the form 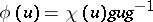 ,
, 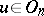 , where
, where 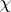 is a fixed homomorphism of
is a fixed homomorphism of 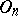 into its centre and
into its centre and 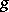 is a fixed bijective semi-linear mapping of
is a fixed bijective semi-linear mapping of 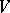 onto itself satisfying
onto itself satisfying 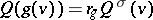 for all
for all 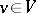 , where
, where 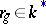 while
while 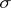 is an automorphism of
is an automorphism of 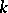 . If
. If 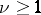 and
and 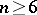 , then every automorphism of
, then every automorphism of 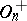 is induced by an automorphism of
is induced by an automorphism of 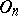 (see [1], [3]).
(see [1], [3]).
Like the other classical groups, an orthogonal group has a geometric characterization (under certain hypotheses). Indeed, let 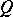 be an anisotropic form such that
be an anisotropic form such that 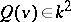 for all
for all 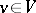 . In this case
. In this case 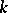 is a Pythagorean orderable field. For a fixed order of the field
is a Pythagorean orderable field. For a fixed order of the field 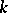 , any sequence
, any sequence 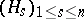 constructed from a linearly independent basis
constructed from a linearly independent basis 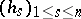 , where
, where 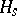 is the set of all linear combinations of the form
is the set of all linear combinations of the form 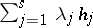 ,
, 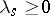 , is called an
, is called an  -dimensional chain of incident half-spaces in
-dimensional chain of incident half-spaces in 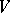 . The group
. The group 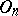 has the property of free mobility, i.e. for any two
has the property of free mobility, i.e. for any two  -dimensional chains of half-spaces there exists a unique transformation from
-dimensional chains of half-spaces there exists a unique transformation from 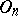 which transforms the first chain into the second. This property characterizes an orthogonal group: If
which transforms the first chain into the second. This property characterizes an orthogonal group: If 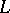 is any ordered skew-field and
is any ordered skew-field and 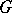 is a subgroup in
is a subgroup in 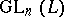 ,
, 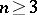 , having the property of free mobility, then
, having the property of free mobility, then 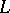 is a Pythagorean field, while
is a Pythagorean field, while 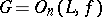 , where
, where 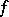 is an anisotropic symmetric bilinear form such that
is an anisotropic symmetric bilinear form such that 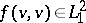 for any vector
for any vector  .
.
Let 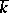 be a fixed algebraic closure of the field
be a fixed algebraic closure of the field 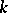 . The form
. The form 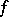 extends naturally to a non-singular symmetric bilinear form
extends naturally to a non-singular symmetric bilinear form 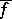 on
on 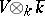 , and the orthogonal group
, and the orthogonal group 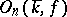 is a linear algebraic group defined over
is a linear algebraic group defined over 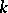 with
with 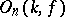 as group of
as group of 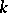 -points. The linear algebraic groups thus defined (for various
-points. The linear algebraic groups thus defined (for various 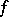 ) are isomorphic over
) are isomorphic over 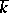 (but in general not over
(but in general not over 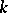 ); the corresponding linear algebraic group over
); the corresponding linear algebraic group over 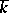 is called the orthogonal algebraic group
is called the orthogonal algebraic group 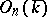 . Its subgroup
. Its subgroup 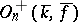 is also a linear algebraic group over
is also a linear algebraic group over 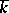 , and is called a properly orthogonal, or special orthogonal algebraic group (notation:
, and is called a properly orthogonal, or special orthogonal algebraic group (notation: 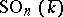 ); it is the connected component of the identity of
); it is the connected component of the identity of 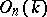 . The group
. The group 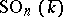 is an almost-simple algebraic group (i.e. does not contain infinite algebraic normal subgroups) of type
is an almost-simple algebraic group (i.e. does not contain infinite algebraic normal subgroups) of type 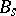 when
when 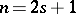 ,
, 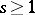 , and of type
, and of type 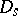 when
when 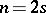 ,
, 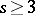 . The universal covering group of
. The universal covering group of 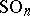 is a spinor group.
is a spinor group.
If 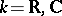 or a
or a 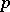 -adic field, then
-adic field, then 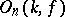 has a canonical structure of a real, complex or
has a canonical structure of a real, complex or 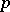 -adic analytic group. The Lie group
-adic analytic group. The Lie group 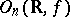 is defined up to isomorphism by the signature of the form
is defined up to isomorphism by the signature of the form 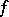 ; if this signature is
; if this signature is 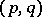 ,
, 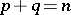 , then
, then 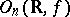 is denoted by
is denoted by 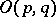 and is called a pseudo-orthogonal group. It can be identified with the Lie group of all real
and is called a pseudo-orthogonal group. It can be identified with the Lie group of all real 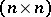 -matrices
-matrices 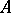 which satisfy
which satisfy
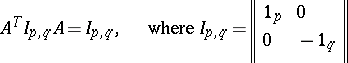 |
(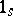 denotes the unit
denotes the unit 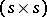 -matrix). The Lie algebra of this group is the Lie algebra of all real
-matrix). The Lie algebra of this group is the Lie algebra of all real 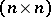 -matrices
-matrices 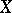 that satisfy the condition
that satisfy the condition 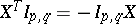 . In the particular case
. In the particular case 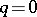 , the group
, the group 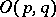 is denoted by
is denoted by 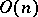 and is called a real orthogonal group; its Lie algebra consists of all skew-symmetric real
and is called a real orthogonal group; its Lie algebra consists of all skew-symmetric real 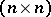 -matrices. The Lie group
-matrices. The Lie group 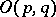 has four connected components when
has four connected components when 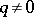 , and two connected components when
, and two connected components when 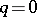 . The connected component of the identity is its commutator subgroup, which, when
. The connected component of the identity is its commutator subgroup, which, when 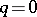 , coincides with the subgroup
, coincides with the subgroup 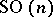 in
in 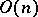 consisting of all transformations with determinant 1. The group
consisting of all transformations with determinant 1. The group 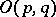 is compact only when
is compact only when 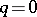 . The topological invariants of
. The topological invariants of 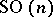 have been studied. One of the classical results is the calculation of the Betti numbers of the manifold
have been studied. One of the classical results is the calculation of the Betti numbers of the manifold 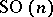 : Its Poincaré polynomial has the form
: Its Poincaré polynomial has the form
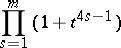 |
when 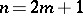 , and the form
, and the form
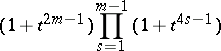 |
when 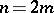 . The fundamental group of the manifold
. The fundamental group of the manifold 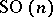 is
is 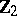 . The calculation of the higher homotopy groups
. The calculation of the higher homotopy groups 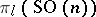 is directly related to the classification of locally trivial principal
is directly related to the classification of locally trivial principal 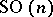 -fibrations over spheres. An important part in topological
-fibrations over spheres. An important part in topological 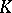 -theory is played by the periodicity theorem, according to which, when
-theory is played by the periodicity theorem, according to which, when 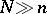 , there are the isomorphisms
, there are the isomorphisms
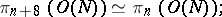 |
further,
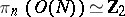 |
if 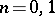 ;
;
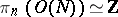 |
if 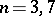 ; and
; and
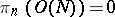 |
if 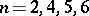 . The study of the topology of the group
. The study of the topology of the group 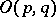 reduces in essence to the previous case, since the connected component of the identity of
reduces in essence to the previous case, since the connected component of the identity of 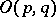 is diffeomorphic to the product
is diffeomorphic to the product 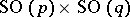 on a Euclidean space.
on a Euclidean space.
References
| [1] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [2] | E. Artin, "Geometric algebra" , Interscience (1957) |
| [3] | , Automorphisms of the classical groups , Moscow (1976) (In Russian; translated from English and French) (Collection of translations) |
| [4] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) |
| [5] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) |
| [6] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) |
| [7] | O.T. O'Meara, "Introduction to quadratic forms" , Springer (1973) |
| [8] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) |
Comments
A Pythagorean field is a field in which the sum of two squares is again a square.
References
| [a1] | J. Dieudonné, "On the automorphisms of the classical groups" , Mem. Amer. Math. Soc. , 2 , Amer. Math. Soc. (1951) |
Orthogonal group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Orthogonal_group&oldid=18142