Hypo-Dirichlet algebra

Let be a uniform algebra on and the algebra of all continuous functions on (cf. also Algebra of functions). The algebra is called a hypo-Dirichlet algebra if the closure of has finite codimension in , and the linear span of is dense in , where 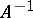is the family of invertible elements of 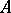. Hypo-Dirichlet algebras were introduced by J. Wermer [a4].

Let 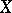be the boundary of a compact subset 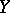in the complex plane whose complement has only finitely many components. Let 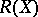be the algebra of all functions on 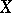that can be uniformly approximated by rational functions with poles off (cf. also Padé approximation; Approximation of functions of a complex variable). Then 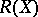is a hypo-Dirichlet algebra [a3].

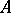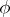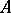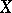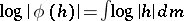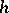Let be a hypo-Dirichlet algebra on and a non-zero complex homomorphism of . If is a representing measure on such that for in 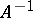, then 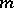is unique. For 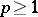, the abstract Hardy space 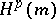is defined as the closure of 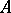in 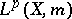(cf. also Hardy spaces). Then a lot of theorems for the concrete Hardy space defined by 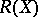are valid for abstract Hardy spaces [a2]. Using such a theory, J. Wermer [a4] showed that if the Gleason part 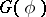of 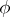is non-trivial (cf. also Algebra of functions), then has an analytic structure.

See also Dirichlet algebra.

References

[a1]	P. Ahern, D. Sarason, "On some hypodirichlet algebras of analytic functions" Amer. J. Math. , 89 (1967) pp. 932–941
[a2]	P. Ahern, D. Sarason, "The 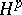spaces of a class of function algebras" Acta Math. , 117 (1967) pp. 123–163
[a3]	H. Barbey, H.König, "Abstract analytic function theory and Hardy algebras" , Lecture Notes Math. : 593 , Springer (1977)
[a4]	J. Wermer, "Analytic disks in maximal ideal spaces" Amer. J. Math. , 86 (1964) pp. 161–170