Booth lemniscate
A plane algebraic curve of order four whose equation in orthogonal Cartesian coordinates is
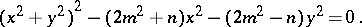 |
If 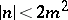 , the Booth lemniscate is called elliptic (it has singular point
, the Booth lemniscate is called elliptic (it has singular point 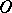 (Fig. a), where
(Fig. a), where 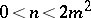 ). If
). If 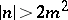 , the Booth lemniscate is called hyperbolic (it has a nodal point at the coordinate origin, cf. Fig. b, where
, the Booth lemniscate is called hyperbolic (it has a nodal point at the coordinate origin, cf. Fig. b, where 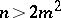 ).
).
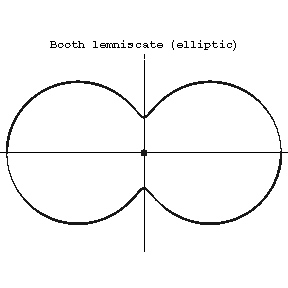
Figure: b017000a
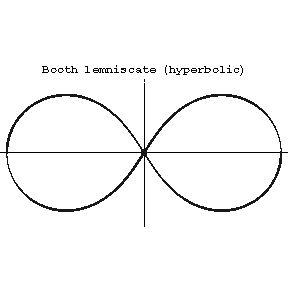
Figure: b017000b
The equation of an elliptic Booth lemniscate in polar coordinates is
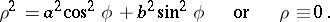 |
If 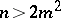 , the equation of a hyperbolic Booth lemniscate has the form
, the equation of a hyperbolic Booth lemniscate has the form
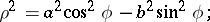 |
and if 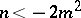
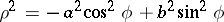 |
 |
The arc length of a Booth lemniscate is expressed by elliptic integrals. The area bounded by an elliptic Booth lemniscate is
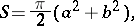 |
while that bounded by a hyperbolic Booth lemniscate is
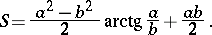 |
The Booth lemniscate is a special case of a Persian curve.
Named after J. Booth [1].
References
| [1] | J. Booth, "A treatise on some new geometrical methods" , 1–2 , London pp. 1873–1877 |
| [2] | A.A. Savelov, "Planar curves" , Moscow (1960) pp. 144–146 (In Russian) |
Booth lemniscate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Booth_lemniscate&oldid=18130