One of the numerical characteristics of a function of several variables. Let 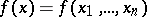 ,
, 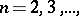 be a function on the
be a function on the  -dimensional parallelepiped
-dimensional parallelepiped
and let
Next, let 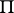 be an arbitrary partition of the parallelepiped by hypersurfaces
be an arbitrary partition of the parallelepiped by hypersurfaces
into  -dimensional parallelepipeds and let
-dimensional parallelepipeds and let 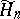 be the class of all functions
be the class of all functions 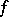 for which
for which
Finally, let 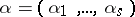 ,
, 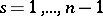 , be an integer-valued vector whose coordinates satisfy the inequalities
, be an integer-valued vector whose coordinates satisfy the inequalities 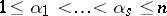 and let
and let 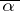 be the integer-valued vector of dimension
be the integer-valued vector of dimension 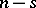 such that its coordinates form a strictly-increasing sequence and consist of all those numbers
such that its coordinates form a strictly-increasing sequence and consist of all those numbers 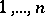 that are not contained among
that are not contained among  . Then every point
. Then every point 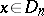 can be written in the form
can be written in the form 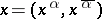 . If the coordinates
. If the coordinates 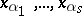 of a point
of a point 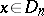 are fixed to the values
are fixed to the values 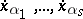 , then one writes
, then one writes 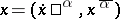 .
.
The Hardy variation of 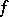 on
on 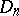 is:
is:
If 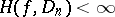 , then one says that the function
, then one says that the function 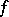 has bounded (finite) Hardy variation on the parallelepiped
has bounded (finite) Hardy variation on the parallelepiped 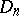 , and the class of all such functions is denoted by
, and the class of all such functions is denoted by 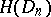 . For
. For 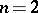 this class was introduced by G.H. Hardy in [1] (see also [2]) in connection with the study of the convergence of Fourier double series. He proved that the rectangular partial sums of the Fourier double series of a function
this class was introduced by G.H. Hardy in [1] (see also [2]) in connection with the study of the convergence of Fourier double series. He proved that the rectangular partial sums of the Fourier double series of a function 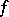 of class
of class 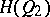 (
(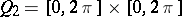 ), of period
), of period 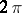 in each variable, converge at every point
in each variable, converge at every point 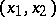 to the number
to the number
where
For a function 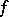 to belong to the class
to belong to the class 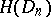 it is necessary and sufficient that it can be represented in the form
it is necessary and sufficient that it can be represented in the form 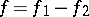 , where
, where 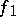 and
and 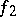 are finite functions on
are finite functions on 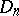 such that
such that 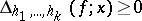 ,
, 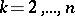 , for all
, for all 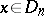 and for all admissible increments
and for all admissible increments 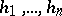 . The class
. The class 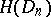 is contained in the class
is contained in the class 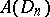 of functions having bounded Arzelà variation on
of functions having bounded Arzelà variation on 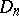 .
.
References
| [1] | G.H. Hardy, "On double Fourier series and especially those which represent the double zeta-function with real and incommensurable parameters" Quarterly J. Math. , 37 (1905) pp. 53–79 |
| [2] | H. Hahn, "Theorie der reellen Funktionen" , 1 , Springer (1921) |
How to Cite This Entry:
Hardy variation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hardy_variation&oldid=18111
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article ,
, 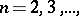 be a function on the
be a function on the  -dimensional parallelepiped
-dimensional parallelepiped
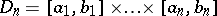
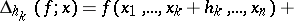
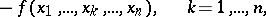
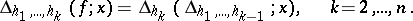
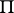 be an arbitrary partition of the parallelepiped by hypersurfaces
be an arbitrary partition of the parallelepiped by hypersurfaces
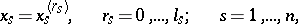
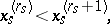

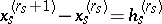
 -dimensional parallelepipeds and let
-dimensional parallelepipeds and let 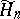 be the class of all functions
be the class of all functions 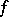 for which
for which
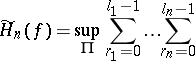
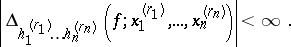
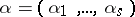 ,
, 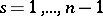 , be an integer-valued vector whose coordinates satisfy the inequalities
, be an integer-valued vector whose coordinates satisfy the inequalities 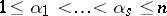 and let
and let 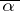 be the integer-valued vector of dimension
be the integer-valued vector of dimension 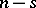 such that its coordinates form a strictly-increasing sequence and consist of all those numbers
such that its coordinates form a strictly-increasing sequence and consist of all those numbers 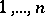 that are not contained among
that are not contained among  . Then every point
. Then every point 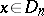 can be written in the form
can be written in the form 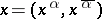 . If the coordinates
. If the coordinates 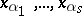 of a point
of a point 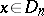 are fixed to the values
are fixed to the values 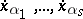 , then one writes
, then one writes 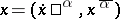 .
.
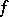 on
on 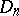 is:
is:
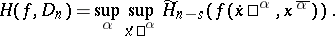
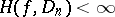 , then one says that the function
, then one says that the function 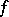 has bounded (finite) Hardy variation on the parallelepiped
has bounded (finite) Hardy variation on the parallelepiped 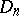 , and the class of all such functions is denoted by
, and the class of all such functions is denoted by 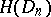 . For
. For 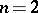 this class was introduced by G.H. Hardy in [1] (see also [2]) in connection with the study of the convergence of Fourier double series. He proved that the rectangular partial sums of the Fourier double series of a function
this class was introduced by G.H. Hardy in [1] (see also [2]) in connection with the study of the convergence of Fourier double series. He proved that the rectangular partial sums of the Fourier double series of a function 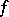 of class
of class 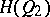 (
(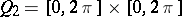 ), of period
), of period 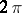 in each variable, converge at every point
in each variable, converge at every point 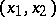 to the number
to the number
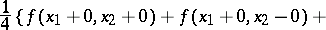
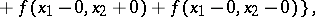
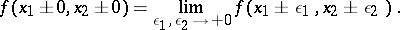
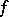 to belong to the class
to belong to the class 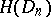 it is necessary and sufficient that it can be represented in the form
it is necessary and sufficient that it can be represented in the form 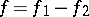 , where
, where 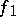 and
and 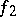 are finite functions on
are finite functions on 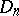 such that
such that 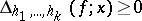 ,
, 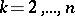 , for all
, for all 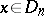 and for all admissible increments
and for all admissible increments 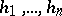 . The class
. The class 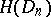 is contained in the class
is contained in the class 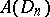 of functions having bounded Arzelà variation on
of functions having bounded Arzelà variation on 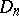 .
.