Frobenius automorphism
An element of a Galois group of a special type. It plays a fundamental role in class field theory. Suppose that 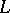 is an algebraic extension of a finite field
is an algebraic extension of a finite field 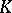 . Then the Frobenius automorphism is the automorphism
. Then the Frobenius automorphism is the automorphism 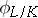 defined by the formula
defined by the formula 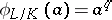 for all
for all 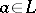 , where
, where 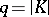 (the cardinality of
(the cardinality of 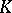 ). If
). If 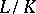 is a finite extension, then
is a finite extension, then 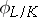 generates the Galois group
generates the Galois group 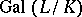 . For an infinite extension
. For an infinite extension 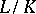 ,
, 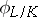 is a topological generator of
is a topological generator of 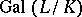 . If
. If 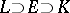 and
and 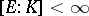 , then
, then 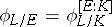 .
.
Suppose that 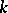 is a local field with a finite residue field
is a local field with a finite residue field 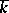 , and that
, and that 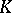 is an unramified extension of
is an unramified extension of 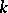 . Then the Frobenius automorphism
. Then the Frobenius automorphism 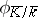 of the extension of residue fields can be uniquely lifted to an automorphism
of the extension of residue fields can be uniquely lifted to an automorphism 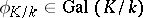 , called the Frobenius automorphism of the unramified extension
, called the Frobenius automorphism of the unramified extension 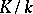 . Let
. Let 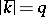 , let
, let 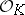 be the ring of integers of
be the ring of integers of 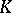 , and let
, and let 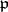 be a maximal ideal in
be a maximal ideal in 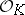 . Then the Frobenius automorphism
. Then the Frobenius automorphism 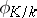 is uniquely determined by the condition
is uniquely determined by the condition 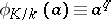
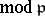 for every
for every 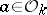 . If
. If 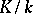 is an arbitrary Galois extension of local fields, then sometimes any automorphism
is an arbitrary Galois extension of local fields, then sometimes any automorphism 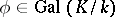 that induces a Frobenius automorphism in the sense indicated above on the maximal unramified subextension of
that induces a Frobenius automorphism in the sense indicated above on the maximal unramified subextension of 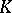 is called a Frobenius automorphism of
is called a Frobenius automorphism of 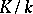 .
.
Let 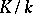 be a Galois extension of global fields, let
be a Galois extension of global fields, let 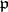 be a prime ideal of
be a prime ideal of 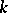 , and let
, and let 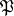 be some prime ideal of
be some prime ideal of 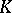 over
over 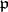 . Suppose also that
. Suppose also that 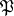 is unramified in
is unramified in 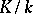 and that
and that 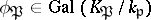 is the Frobenius automorphism of the unramified extension of local fields
is the Frobenius automorphism of the unramified extension of local fields 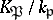 . If one identifies the Galois group
. If one identifies the Galois group 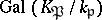 with the decomposition subgroup of
with the decomposition subgroup of 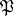 in
in 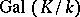 , one can regard
, one can regard 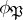 as an element of
as an element of 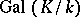 . This element is called the Frobenius automorphism corresponding to the prime ideal
. This element is called the Frobenius automorphism corresponding to the prime ideal 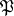 . If
. If 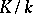 is a finite extension, then, according to the Chebotarev density theorem, for any automorphism
is a finite extension, then, according to the Chebotarev density theorem, for any automorphism 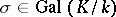 there is an infinite number of prime ideals
there is an infinite number of prime ideals 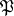 , unramified in
, unramified in 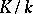 , such that
, such that 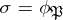 . For an Abelian extension
. For an Abelian extension 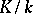 , the element
, the element 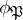 depends only on
depends only on 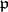 . In this case
. In this case 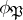 is denoted by
is denoted by 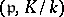 and is called the Artin symbol of the prime ideal
and is called the Artin symbol of the prime ideal 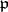 .
.
References
| [1] | A. Weil, "Basic number theory" , Springer (1974) |
Frobenius automorphism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Frobenius_automorphism&oldid=18099