Transversal system
transversal design, transversal scheme, 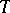 -system
-system
A system 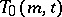 of sets defined for a given collection of
of sets defined for a given collection of 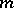 pairwise-disjoint finite sets
pairwise-disjoint finite sets 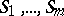 , each of which has cardinality
, each of which has cardinality 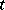 . Namely: a transversal system
. Namely: a transversal system 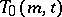 is a system of
is a system of 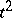 sets
sets 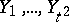 (blocks or transversals), containing
(blocks or transversals), containing 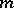 elements each and such that:
elements each and such that:
1) 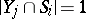 ;
; 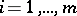 ;
; 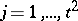 ;
;
2) 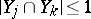 for
for 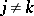 .
.
In a transversal design, any two elements  and
and 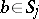 ,
, 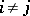 , occur together in exactly one block. The existence of a transversal design
, occur together in exactly one block. The existence of a transversal design 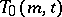 is equivalent to the existence of an orthogonal array
is equivalent to the existence of an orthogonal array 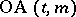 .
.
Transversal designs are used in recursive constructions of block designs (cf. Block design).
A set of 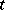 transversals in
transversals in 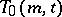 is called parallel if no two of them intersect. If a transversal design
is called parallel if no two of them intersect. If a transversal design 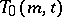 contains
contains  (or more) parallel classes, then it is denoted by
(or more) parallel classes, then it is denoted by 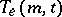 .
.
Some of the basic properties of transversal systems are:
a) if 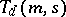 and
and 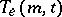 exist, then so does
exist, then so does 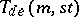 ;
;
b) 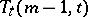 exists if and only if
exists if and only if 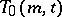 exists.
exists.
References
| [1] | M. Hall, "Combinatorial theory" , Wiley (1986) |
| [2] | H. Hanani, "The existence and construction of balanced incomplete block designs" Ann. Math. Stat. , 32 (1961) pp. 361–386 |
Comments
The finite sets 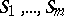 making up the design are called point classes or point groups.
making up the design are called point classes or point groups.
The existence of a transversal design 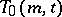 is equivalent to the existence of
is equivalent to the existence of 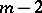 mutually orthogonal Latin squares of order
mutually orthogonal Latin squares of order 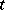 . If a
. If a 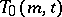 exists, and
exists, and 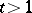 , then
, then 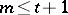 .
.
See also [a1]–[a3] for the recursive construction of and existence results for transversal designs (and of their generalization "transversal design with holes" , [a2]).
One of the most important results on recursive construction of transversal designs (due to R.M. Wilson [a4], see also [a1]) is as follows:
Let 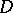 be a
be a 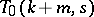 with point classes
with point classes  and
and 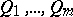 , let
, let 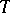 be a
be a 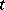 -subset of
-subset of 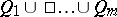 and put
and put 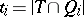 for
for 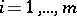 , and
, and  for every block
for every block 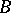 of
of 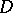 . Assume the existence of
. Assume the existence of  for
for 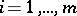 and of
and of 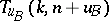 for each block
for each block 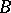 of
of 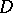 . Then
. Then  also exists.
also exists.
Transversals designs (and their dual structures, nets) are also of considerable geometric and algebraic interest. For instance, a 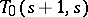 is equivalent to an affine or projective plane of order
is equivalent to an affine or projective plane of order  , and a
, and a 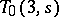 is basically the same as a quasi-group of order
is basically the same as a quasi-group of order  . Thus, the geometric and algebraic properties of transversal designs (including the study of their automorphism groups) have found considerable interest, cf. [a4].
. Thus, the geometric and algebraic properties of transversal designs (including the study of their automorphism groups) have found considerable interest, cf. [a4].
References
| [a1] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1986) |
| [a2] | A.E. Brouwer, "Recursive constructions of mutually orthogonal Latin squares" Ann. Discr. Math. , 46 (1991) pp. 149–168 |
| [a3] | D. Jungnickel, "Latin squares, their geometries and their groups: a survey" D. Ray-Chaudhuri (ed.) , Coding Theory and Design Theory , IMA Vol. Math. Appl. , 21 , Springer (1990) pp. 166–225 |
| [a4] | R.M. Wilson, "Concerning the number of mutually orthogonal Latin squares" Discr. Math. , 9 (1974) pp. 181–198 |
| [a5] | H. Hanani, "Balanced incomplete block designs and related designs" Discrete Math. , 11 (1975) pp. 255–369 |
Transversal system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transversal_system&oldid=18087